练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （本题7分）如图，等腰直角△ABC中，∠ABC=90°，点D在AC上， 将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.

     

     

     

    ⑴求∠DCE的度数；

    ⑵当AB=4，AD:DC=1: 3时，求DE的长.

     

    【答案】

    解：（1）∵△CBE是由△ABD旋转得到的，∴△ABD≌△CBE，…………1分

    ∴∠A＝∠BCE＝45°，……………………………………………………………2分

    ∴∠DCE＝∠DCB＋∠BCE＝90° ………………………………………………3分

    （2）∵在等腰直角三角形ABC中，∵AB＝４，∴AC＝４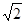……………………4分

    又∵AD︰DC＝１︰3,∴AD=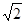,DC=3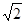,…………………………………………5分

    由（１）知AD＝CE且∠DCE＝90°, ………………………………………………6分

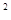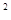    ∴DE＝DC＋CE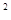＝2＋18＝20，∴DE＝2   …………………………………7分

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

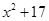    （本题8分）如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为（）cm，正六边形的边长为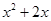（）cm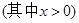.求这两段铁丝的总长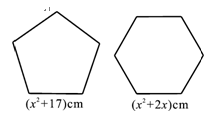

    查看答案和解析>>

    科目：初中数学 来源：2011-2012年江苏省江阴初级中学九年级上学期期中考试数学卷 题型：解答题

    （本题8分）如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为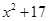（）cm，正六边形的边长为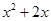（）cm.求这两段铁丝的总长

    查看答案和解析>>

    科目：初中数学 来源：2012年河南省中考模拟试题数学卷 题型：解答题

    （本题8分）如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.

     

    查看答案和解析>>

    科目：初中数学 来源：2013届浙江省杭州市萧山区临浦片八年级上学期期中质量检测数学卷 题型：解答题

     

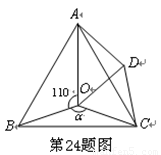
    （本题12分）如图，点O是等边△ABC内一点，D是△ABC外的一点， ∠AOB= 110°，

    ∠BOC= 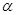，△BOC ≌△ADC，∠OCD＝60°，连接OD。

    （1）求证：△OCD是等边三角形；

    （2）当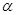＝150°时，试判断△AOD 的形状，并说明理由；

    （3）探究：当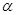为多少度时，△AOD是等腰三角形。

     

     

     

     

     

     

     

    查看答案和解析>>

    科目：初中数学 来源：2011届山东省滨州市滨城区九年级第一学期期中学业水平测试数学卷 题型：解答题

    （本题12分）如图，两个同样大小的等边△ABC和△ACD，边长为a，它们拼成一个菱形ABCD，另一个足够大的等边△AEF绕点A旋转，AE与BC相交于点M，AF与CD相交于点N。

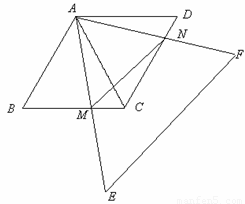
    1.（1）证明：∠DAN=∠CAM;

    2.（2）求四边形AMCN的面积；

    3.（3）探索△AMN何时面积最小，并写出这个最小面积的值.

     

    查看答案和解析>>

    同步练习册答案