
 如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.
如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.分析 (1)由平行四边形的性质易得AC=BM=BD,∠BDC=∠M=∠ACD,由全等三角形判定定理及性质得出结论;
(2)连接EH,HF,FG,GE,E,F,G,H分别是AB,CD,AC,BD的中点,易得四边形HFGE为平行四边形,由平行四边形的性质及(1)结论得?HFGE为菱形,易得EF与GH互相垂直平分.
解答 证明:(1)过点B作BM∥AC交DC的延长线于点M,如图1,
∵AB∥CD
∴四边形ABMC为平行四边形,
∴AC=BM=BD,∠BDC=∠M=∠ACD,
在△ACD和△BDC中,
$\left\{\begin{array}{l}{AC=BD}\\{∠ACD=∠BDC}\\{CD=DC}\end{array}\right.$,
∴△ACD≌△BDC(SAS),
∴AD=BC;
(2)连接EH,HF,FG,GE,如图2,
∵E,F,G,H分别是AB,CD,AC,BD的中点,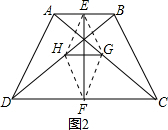
∴HE∥AD,且HE=$\frac{1}{2}$AD,FG∥AD,且FG=$\frac{1}{2}AD$,
∴四边形HFGE为平行四边形,
由(1)知,AD=BC,
∴HE=EG,
∴?HFGE为菱形,
∴EF与GH互相垂直平分.
点评 本题主要考查了平行四边形的性质及判定,全等三角形的性质与判定,菱形的判定及性质,综合运用平行四边形的性质及判定,全等三角形的性质与判定是解答此题的关键.


科目:初中数学 来源: 题型:解答题
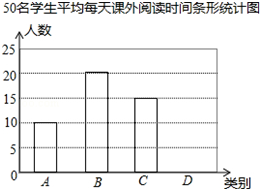 课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:| 类别 | 时间t(小时) | 人数 |
| A | t<0.5 | 10 |
| B | 0.5≤t<1 | 20 |
| C | 1≤t<1.5 | 15 |
| D | t≥1.5 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
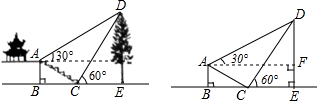
 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为2$\sqrt{3}$或2$\sqrt{7}$或2.
如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为2$\sqrt{3}$或2$\sqrt{7}$或2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
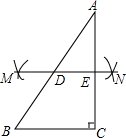 已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 上升时间/min | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/m | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/m | 20 | 30 | … | 0.5x+15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
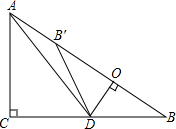 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com