练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．在实数$\frac{22}{7}$，-$\sqrt{3}$，-3.14，0，π，2.1611 611 61…，$\root{3}{9}$中，无理数有（　　）
    A．1 个B．2个C．3个D．4个

    分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．

    解答 解：-$\sqrt{3}$，π，2.1611 611 61…，$\root{3}{9}$是无理数，
    故选：D．

    点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．下列说法正确的是（　　）
    A．两个数之差一定小于被减数B．减去一个负数，差一定大于被减数
    C．减去一个正数，差一定大于被减数D．0减去任何数，差都是负数

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数，一次函数，二次函数都是特殊的幂函数，当α为3时，y=x3的图象如图所示，则下列说法中：
    ①y随x的增大而增大；
    ②当x＜0时，y＜0；
    ③若点（a，b）在y=x3的图象上，则（-a，-b）也一定在它的图象上；
    ④若点（x1，y1），（x2，y2），（$\frac{{x}_{1}+{x}_{2}}{2}$，y3）都在y=x3的图象上（x1x2＞0），则有$\frac{{y}_{1}+{y}_{2}}{2}$≤y3．
    正确的有：①②③（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，∠AOB=∠COD=90°，∠BOC与∠AOD相等吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

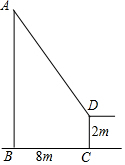    16．如图，小华将升旗的绳子拉紧到旗杆底端点B，绳子末端刚好接触到地面，然后拉紧绳子使其末端到点D处，点D到地面的距离CD长为2m，点D到旗杆AB的水平距离为8m，若设旗杆的高度AB长为xm，则根据题意所列的方程是（　　）
    A．（x-2）2+82=x2B．（x+2）2+82=x2C．x2+82=（x-2）2D．x2+82=（x+2）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．一次会议上，每两个参加会议的人都相互握一次手，有人统计一共握了36次手，设到会的人数为x人，则根据题意列方程为$\frac{1}{2}$x（x-1）=36．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图所示，在△ABC中，∠B=90°，点P从点B开始沿BA边向点A以1厘米/秒的宽度移动；同时，点Q也从点B开始沿BC边向点C以2厘米/秒的速度移动，问几秒后，△PBQ的面积为36平方厘米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．在平面直角坐标系中，点O为原点，点A的坐标为（0，3），以点A为圆心，OA为半径在y轴右侧作半圆A，直线l：y=x+m交x轴于点C．
    （1）如图1，当m=0时，直线l与半圆A分别相交于点O，D，求此时OD的长；
    （2）当m=-3时，在半圆A上取一点P，过点P作PH⊥l于点H．
    ①如图2，当直线PH与半圆A相切时，求此时点P的坐标；
    ②如图3，设点P的坐标为（a，b），过点P作PE⊥y于点E，连接EH，△PEH的其中两边之比能否为$\sqrt{2}$：1？若能，求此时a与b的关系；若不能，请说明理由．

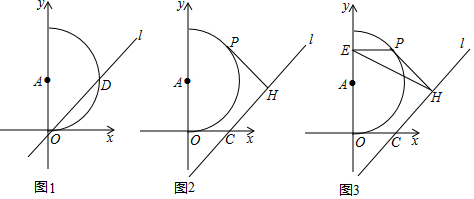
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．计算：（-2）200+（-2）201所得的结果是（　　）
    A．2200B．-1C．-2200D．-2

    查看答案和解析>>

    同步练习册答案