Question

3．问题发现：
（1）在我们学习过的几何图形里，有很多图形的面积和周长能同时被某条直线平分，如图1，⊙O的周长和面积能被过圆心的任意一条直线平分．请你在图2和图3中分别作两条不同的直线将矩形ABCD和梯形ABCD的周长和面积同时平分，并简要说明做法．
问题解决：
如图4，在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10，点E在下底边BC上，点F在腰AB上．
（2）是否存在线段EF将等腰梯形ABCD的周长和面积平分？若存在，求出此时BE的长，若不存在，请说明理由．
（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1：2的两部分？若存在，求出此时BE的长，若不存在，请说明理由．

Answer 1

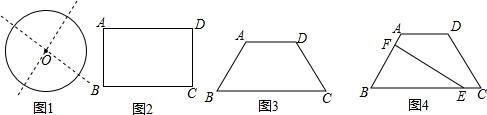
分析 （1）过矩形的对角的顶点的直线即可平分矩形的面积和周长；过对角线BD的中点O的直线即可平分矩形的面积和周长；取梯形上、下底的中点M、N，过M、N作直线即可将梯形的面积和周长平分；过顶点A和MN的中点O的直线即可将梯形的面积和周长平分；
（2）先作AK⊥BC于K，FG⊥BC于G，根据等腰梯形的性质，可得BK=$\frac{1}{2}$（BC-AD）=$\frac{1}{2}$×（10-4）=3，在Rt△ABK中，利用勾股定理可求出AK=4，由于AK、FG垂直于同一直线故平行，可得比例线段，求出FG=$\frac{12-x}{5}$×4，利用面积公式可得S_△BEF=$\frac{1}{2}$BE•FG=-$\frac{2}{5}$x²+$\frac{24}{5}$x（7≤x≤10，因为BF最大取5，故BE最小取7，又不能超过10）；根据线段EF将等腰梯形ABCD的周长和面积平分，可以得到$\frac{1}{2}$S_梯形ABCD=-$\frac{2}{5}$x²+$\frac{24}{5}$x，即14=-$\frac{2}{5}$x²+$\frac{24}{5}$x，解得x₁=7，x₂=5（不合题意，舍去）；
（3）仍然按照（2）的步骤和方法去做就可以了，注意不是分成相等的两份，而是1：2就可以了，得到关于x的一元二次方程，先求出根的判别式△，由于△＜0，故不存在实数根．

解答 解：（1）①过矩形的对角的顶点的直线即可平分矩形的面积和周长；过对角线BD的中点O的直线即可平分矩形的面积和周长；
②取上、下底的中点M、N，过M、N作直线即可将梯形的面积和周长平分；过顶点A和MN的中点O的直线即可将梯形的面积和周长平分；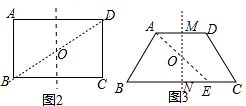

（2）存在；
由已知条件得：
梯形周长为24，高4，面积为28．
过点F作FG⊥BC于G
∴BK=$\frac{1}{2}$（BC-AD）=$\frac{1}{2}$×（10-4）=3，
∴AK=$\sqrt{A{B}^{2}-B{K}^{2}}$=4，
∵EF平分等腰梯形ABCD的周长，设BE长为x，
∴BF=12-x，
过点A作AK⊥BC于K
∴△BFG∽△BAK，
∴$\frac{FG}{AK}$=$\frac{BF}{BA}$，
即：$\frac{FG}{4}$=$\frac{12-x}{5}$，
则可得：FG=$\frac{12-x}{5}$×4
∴S_△BEF=$\frac{1}{2}$BE•FG=-$\frac{2}{5}$x²+$\frac{24}{5}$x（7≤x≤10），
∵线段EF将等腰梯形ABCD的周长和面积平分，
$\frac{1}{2}$S_梯形ABCD=-$\frac{2}{5}$x²+$\frac{24}{5}$x，
即-$\frac{2}{5}$x²+$\frac{24}{5}$x=14，
x²-12x+35=0，
（x-7）（x-5）=0，
解得x₁=7，x₂=5（不合题意舍去）
∴存在线段EF将等腰梯形ABCD的周长与面积同时平分，此时BE=7；

（3）不存在；
假设存在，第一种情况：显然是：S_△BEF：S_AFECD=1：2，（BE+BF）：（AF+AD+DC+CE）=1：2，
梯形ABCD周长的三分之一为$\frac{24}{3}$=8，面积的三分之一为$\frac{28}{3}$．因为BE=x，
所以BF=（8-x）
∵FM∥AH，
∴△FBM∽△ABH，
∴BF：AB=FM：AH，
∴$\frac{8-x}{5}$=$\frac{FM}{4}$，
∴FM=$\frac{32-4x}{5}$，
∴△BEF的面积=-$\frac{2}{5}$x²+$\frac{16}{5}$x，
当$\frac{1}{3}$S_{梯形ABCD的面积}=$\frac{28}{3}$时，
∴$\frac{28}{3}$=-$\frac{2}{5}$x²+$\frac{16}{5}$x，
整理方程得：-3x²+24x-70=0，
△=576-840＜0
∴不存在这样的实数x．
即不存在线段EF将等腰梯形ABCD的周长和面积同时分成1：2的两部分．
第二种情况：显然是：S_△BEF：S_AFECD=2：1，（BE+BF）：（AF+AD+DC+CE）=1：2，
梯形ABCD周长的三分之一为$\frac{24}{3}$=8，面积的三分之一为$\frac{28}{3}$．因为BE=x，
所以BF=（8-x）
∵FM∥AH，
∴△FBM∽△ABH，
∴BF：AB=FM：AH，
∴$\frac{8-x}{5}$=$\frac{FM}{4}$，
∴FM=$\frac{32-4x}{5}$，
∴△BEF的面积=-$\frac{2}{5}$x²+$\frac{16}{5}$x，
当$\frac{1}{3}$S_{梯形ABCD的面积}=$\frac{28}{3}$时，
∴$\frac{28}{3}$×2=-$\frac{2}{5}$x²+$\frac{16}{5}$x，
整理方程得：3x²-24x+140=0，
△＜0
∴不存在这样的实数x．
即不存在线段EF将等腰梯形ABCD的周长和面积同时分成1：2的两部分．

点评 本题是四边形的综合题，综合利用了等腰梯形的性质、垂直于同一直线的两直线平行，勾股定理，三角形、梯形面积公式，解一元二次方程，以及一元二次方程根的判别式等知识．