
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.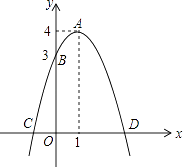
(1)求此抛物线的解析式;
(2)求C,D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD= ![]() S△BCD , 求点P的坐标.
S△BCD , 求点P的坐标.
【答案】
(1)
解:∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4
(2)
解:由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD= ![]() CD×|yB|=
CD×|yB|= ![]() ×4×3=6
×4×3=6
(3)
解:由(2)知,S△BCD= ![]() CD×|yB|=
CD×|yB|= ![]() ×4×3=6;CD=4,
×4×3=6;CD=4,
∵S△PCD= ![]() S△BCD,
S△BCD,
∴S△PCD= ![]() CD×|yP|=
CD×|yP|= ![]() ×4×|yP|=3,
×4×|yP|=3,
∴|yP|= ![]() ,
,
∵点P在x轴上方的抛物线上,
∴yP>0,
∴yP= ![]() ,
,
∵抛物线的解析式为y=﹣(x﹣1)2+4;
∴ ![]() =﹣(x﹣1)2+4,
=﹣(x﹣1)2+4,
∴x=1± ![]() ,
,
∴P(1+ ![]() ,
, ![]() ),或P(1﹣
),或P(1﹣ ![]() ,
, ![]() )
)
【解析】(1)设抛物线顶点式解析式y=a(x﹣1)2+4,然后把点B的坐标代入求出a的值,即可得解;(2)令y=0,解方程得出点C,D坐标,再用三角形面积公式即可得出结论;(3)先根据面积关系求出点P的坐标,求出点P的纵坐标,代入抛物线解析式即可求出点P的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题.
某校学生积极为地震灾区捐款奉献爱心.小颖随机抽查其中30名学生的捐款情况如下:(单位:元)2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、50.
(1)这30名学生捐款的最大值、最小值、极差、平均数各是多少?
(2)将30名学生捐款额分成下面5组,请你完成频数统计表:
(3)根据上表,作出频数分布直方图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,∠BAD=∠DCB,若不增加任何字母和辅助线,要使得四边形ABCD是矩形,则还需要增加一个条件是_______________.
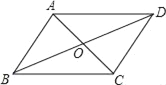
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连结MN,作AH⊥MN,垂足为点H
(1)如图1,猜想AH与AB有什么数量关系?并证明;
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;
小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标;
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形 
(1)求证:△DFB是等腰三角形;
(2)若DA= ![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com