Question

1．如图，在Rt△AOB中，∠AOB=90°，OA=OB=2，点D，E分别是OA，OB边的中点，若正方形OCDE绕点O按逆时针方向旋转，得到正方形OD₁C₁E₁，记旋转角为α．
（1）如图①，当α=90°时，线段AD₁的长度是$\sqrt{5}$，线段BE₁的长度是$\sqrt{5}$；
（2）如图②，当α=135°时，求证：AD₁=BE₁，且AD₁⊥BE₁；
（3）若直线AD₁与直线BE₁相交于点M，填空；
         ①线段MC的长为$\sqrt{2}$；
         ②点M到直线OA的距离的最大值为$\frac{1+\sqrt{3}}{2}$．

Answer 1

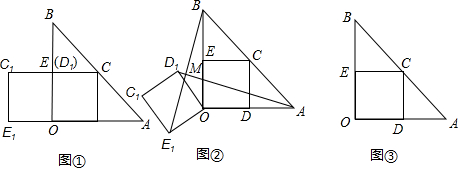
分析 （1）由已知条件得出OE=OD=1，由旋转的性质得当α=90°时，OE₁=1，∠AOE=90°，由勾股定理求出AD₁=BE₁=$\sqrt{5}$即可；
（2）由旋转的性质得出OD₁=OE₁，∠AOD₁=∠BOE₁=135°，由SAS证明△AOD₁≌△BOE，得出AD₁=BE₁，∠OAD₁=∠OBE₁，由对顶角相等和三角形内角和定理得出∠BMA=∠AOM=90°，即可证出AD₁⊥BE₁；
（3）①由勾股定理求出AB，由直角三角形的性质得出MC的长；
②作MG⊥OA于G，D₁、E₁在以A为圆心，OD为半径的圆上，当直线AD₁与BE₁的交点M到直线OA的距离最大，此时四边形OD₁ME₁是正方形，MD₁=1，则AD₁=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，证出∠OAM=30°，得出AM=1+$\sqrt{3}$，由直角三角形的性质得出MG=$\frac{1}{2}$AM=$\frac{1+\sqrt{3}}{2}$．

解答 （1）解：∵∠AOB=90°，OA=OB=2，点D，E分别是OA，OB边的中点，
∴OE=OD=1，
∵正方形OCDE绕点O按逆时针方向旋转，得到正方形OD₁C₁E₁，旋转角为α．
∴当α=90°时，
，OE₁=1，∠AOE=90°，
∴AD₁=BE₁=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$；
故答案为：$\sqrt{5}$，$\sqrt{5}$；

（2）证明：∵正方形OCDE绕点O按逆时针方向旋转，得到正方形OD₁C₁E₁，旋转角为α=135°．
∴OD₁=OE₁，∠AOD₁=∠BOE₁=135°，
在△AOD₁和△BOE₁中，$\left\{\begin{array}{l}{O{D}_{1}=O{E}_{1}}&{\;}\\{∠AO{D}_{1}=∠BO{E}_{1}}&{\;}\\{OA=OB}&{\;}\end{array}\right.$，
∴△AOD₁≌△BOE（SAS），
∴AD₁=BE₁，∠OAD₁=∠OBE₁，
∵∠ANO=∠BND₁，
由三角形内角和定理得：∠BMA=∠AOM=90°，
∴AD₁⊥BE₁；

（3）解：①∵∠AOB=90°，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$∵∠BMA=90°，BC=AC，
∴MC=$\frac{1}{2}$AB=$\sqrt{2}$；
故答案为：$\sqrt{2}$；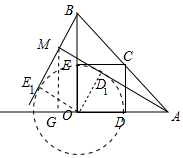
②作MG⊥OA于G，
∵D₁、E₁在以A为圆心，OD为半径的圆上，
当直线AD₁与BE₁的交点M到直线OA的距离最大，
此时四边形OD₁ME₁是正方形，MD₁=1，
则AD₁=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴∠OAM=30°，
∴AM=1+$\sqrt{3}$，
∴MG=$\frac{1}{2}$AM=$\frac{1+\sqrt{3}}{2}$；
故答案为：$\frac{1+\sqrt{3}}{2}$．

点评 本题是四边形综合题目，考查了等腰直角三角形的性质、正方形的性质、旋转的性质、全等三角形的判定与性质、勾股定理、三角形内角和定理等知识；本题综合性强，有一定难度．