
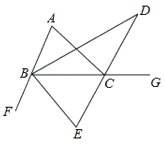
【题目】如图,![]() 是
是![]() 的外角,
的外角,![]() 的平分线所在的直线分别与
的平分线所在的直线分别与![]()
![]() 的平分线
的平分线![]() 交于点
交于点![]() .
.
![]() 若
若![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() 求
求![]() ;
;
![]() 连接
连接![]() 若
若![]() 则
则![]() _
_
【答案】(1)∠D=35°;(2)∠E=90°![]() α;(3)
α;(3)![]()
【解析】
(1)由角平分线的定义得到∠DCG=![]() ∠ACG,∠DBC=
∠ACG,∠DBC=![]() ∠ABC,然后根据三角形外角的性质求出2∠DCG=∠A+2∠DBC,2∠DCG=2∠D+2∠DBC,等量代换即可得出答案;
∠ABC,然后根据三角形外角的性质求出2∠DCG=∠A+2∠DBC,2∠DCG=2∠D+2∠DBC,等量代换即可得出答案;
(2)由(1)知∠D=![]() ∠A=
∠A=![]() α,求出∠DBE=90°,即可求得∠E;
α,求出∠DBE=90°,即可求得∠E;
(3)如图,连接AD,过点D作DN⊥BG于N,DM⊥BA交BA的延长线于M,过点D作DQ⊥AC于Q,根据角平分线的判定和性质证得AD是∠MAC的角平分线,然后利用三角形外角的性质求出∠MAD=![]() ∠MAC=
∠MAC=![]() ,∠MAD=∠ABD+∠ADB=
,∠MAD=∠ABD+∠ADB=![]() +∠ADB,等量代换即可求出答案.
+∠ADB,等量代换即可求出答案.
解:(1)∵CD平分∠ACG,BD平分∠ABC,
∴∠DCG=![]() ∠ACG,∠DBC=
∠ACG,∠DBC=![]() ∠ABC,
∠ABC,
∵∠ACG=∠A+∠ABC,
∴2∠DCG=∠A+∠ABC=∠A+2∠DBC,
∵∠DCG=∠D+∠DBC,
∴2∠DCG=2∠D+2∠DBC,
∴∠A+2∠DBC=2∠D+2∠DBC,
∴∠D=![]() ∠A=35°;
∠A=35°;
(2)由(1)知∠D=![]() ∠A=
∠A=![]() α,
α,
∵∠DBE=∠DBC+∠CBE=![]() ∠ABC+
∠ABC+![]() ∠CBF=
∠CBF=![]() (∠ABC+∠CBF)=
(∠ABC+∠CBF)=![]() ×180°=90°,
×180°=90°,
∴∠E=90°-∠D=90°![]() α;
α;
(3)如图,连接AD,过点D作DN⊥BG于N,DM⊥BA交BA的延长线于M,过点D作DQ⊥AC于Q,
∵BD是∠ABC的平分线,CD是∠ACG的平分线,
∴DM=DN,DQ=DN,
∴DM=DQ,
∵DM⊥AM,DQ⊥AC,
∴AD是∠MAC的角平分线,
∵∠MAC=∠ACB+∠ABC=β+∠ABC,
∴∠MAD=![]() ∠MAC=
∠MAC=![]() ,
,
又∵∠MAD=∠ABD+∠ADB=![]() +∠ADB,
+∠ADB,
∴![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
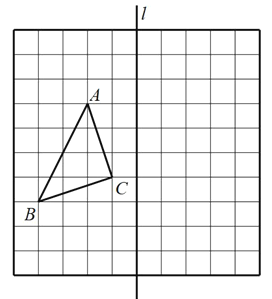
【题目】如图,点![]() 、
、![]() 、
、![]() 都在方格纸的格点上,方格纸中每个小正方形的边长都是1.
都在方格纸的格点上,方格纸中每个小正方形的边长都是1.
(1)画![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(2)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 最小;(要求在直线
最小;(要求在直线![]() 上标出点
上标出点![]() 的位置)
的位置)
(3)连接![]() 、
、![]() ,计算四边形PABC的面积.
,计算四边形PABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观, 从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形积的方法进行直 观推导和解释.

![]() 如图 1,是一个重要公式的几何解释,请你写出这个公式:
如图 1,是一个重要公式的几何解释,请你写出这个公式:
![]() 如图 2,在
如图 2,在![]() 中,
中,![]() ,以
,以![]() 的三边长向外作正方形的面积分别为
的三边长向外作正方形的面积分别为![]() ,试猜想
,试猜想![]() 之间存在的等量关系,直接写出结论 .
之间存在的等量关系,直接写出结论 .
![]() 如图 3,如果以
如图 3,如果以![]() 的三边长
的三边长![]() 为直径向外作半圆,那么第
为直径向外作半圆,那么第![]() 问的结论 是否成立?请说明理由.
问的结论 是否成立?请说明理由.
![]() 如图 4,在
如图 4,在![]() 中,
中,![]() ,三边分别为
,三边分别为![]() ,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
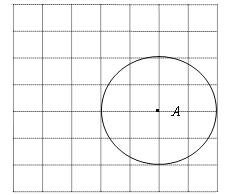
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
(1)根据A点坐标建立平面直角坐标系;
(2)将⊙A向左平移____________个单位长度与y轴首次相切,得到⊙A,并画出⊙A.此时点A的坐标为_____________.
(3)求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列事件发生的概率标在图中:
(1)从高处抛出的物体必落到地面;
(2)从装有![]() 个红球的袋子中任取一个,取出的球是白球;
个红球的袋子中任取一个,取出的球是白球;
(3)月亮绕着地球转;
(4)从装有![]() 个红球、
个红球、![]() 个白球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同);
个白球的口袋中任取一个球,恰好是红球(这些球除颜色外完全相同);
(5)三名选手抽签决定比赛顺序(有三个签,分别写有![]() ,
,![]() ,
,![]() ),抽到写有
),抽到写有![]() 的签.
的签.
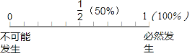
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com