Question

7．如图，在菱形ABCD中，∠BAD=60°，△AEF为等边三角形，且点B在直线EF上运动．
（1）如图1，当点B在线段EF上时，∠ADF-∠BAF的度数为60°．
（2）如图2，当点B在EF的延长线上时，写出∠ADF，∠BAF，∠AFE之间的数量关系，并说明理由；
（3）在（2）的条件下，求线段BF、AB、BE之间的数量关系．

Answer 1

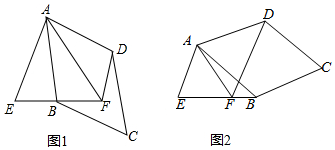
分析 （1）证明△EAB≌△FAD（SAS），得∠ABE=∠ADF，再利用外角定理得：∠ABE=∠BAF+∠AFE，经过变形后可得结论；
（2）同理得：△EAB≌△FAD，再利用外角定理可得结论；
（3）设BE=y，BF=x，则AE=EF=y-x，根据三角函数表示AG=$\frac{\sqrt{3}}{2}$（y-x），EG=$\frac{1}{2}$（y-x），BG=$\frac{1}{2}$x+$\frac{1}{2}$y，由勾股定理得：AB²=BG²+AG²，列式计可．

解答 解：（1）如图1，∵△AEF是等边三角形，
∴AE=AF，∠EAF=∠AFE=60°，
∵四边形ABCD是菱形，
∴AB=AD，
∵∠BAD=60°，
∴∠EAF=∠BAD，
∴∠EAF-∠BAF=∠BAD-∠BAF，
即∠EAB=∠FAD，
∴△EAB≌△FAD（SAS），
∴∠ABE=∠ADF，
∵∠ABE=∠BAF+∠AFE，
∴∠ABE-∠BAF=∠AFE=60°，
∴∠ADF-∠BAF=60°，
故答案为：60°；

（2）∠AFE=∠ADF+∠BAF，理由是：
如图2，同理得：△EAB≌△FAD，
∴∠ADF=∠ABE，
∵∠AFE=∠ABE+∠BAF，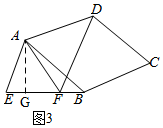
∴∠AFE=∠ADF+∠BAF；

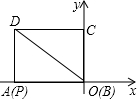
（3）AB²=BE²+BF²-BE•BF，理由是：
如图3，过A作AG⊥BE于G，
设BE=y，BF=x，则AE=EF=y-x，
在Rt△AEG中，sin∠E=sin60°=$\frac{AG}{AE}$，
∴AG=$\frac{\sqrt{3}}{2}$（y-x），
EG=$\frac{1}{2}$（y-x），
∴BG=BE-EG=y-$\frac{1}{2}$（y-x）=$\frac{1}{2}$x+$\frac{1}{2}$y，
由勾股定理得：AB²=BG²+AG²，
AB²=（$\frac{1}{2}$x+$\frac{1}{2}$y）²+[$\frac{\sqrt{3}}{2}$（y-x）]²，
AB²=x²+y²-xy，
∴AB²=BE²+BF²-BE•BF．

点评 本题是四边形的综合题，考查了菱形的性质、三角形全等的性质和判定、勾股定理、三角函数，第三问较了复杂，作辅助线，设BE=y，BF=x，利用三角函数表示其它各边是关键．