
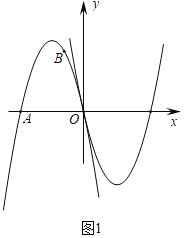
【题目】如图1,抛物线![]() 经过点
经过点![]() 、
、![]() 两点,
两点,![]() 是其顶点,将抛物线
是其顶点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
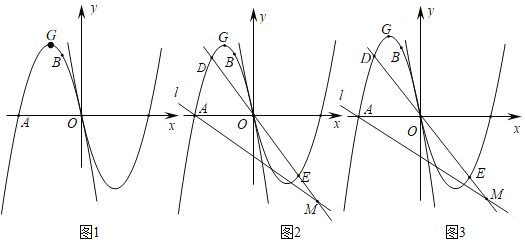
(1)求抛物线![]() 的函数解析式及顶点
的函数解析式及顶点![]() 的坐标;
的坐标;
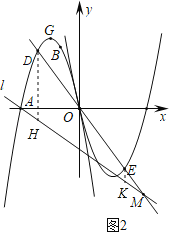
(2)如图2,直线![]() 经过点
经过点![]() ,
,![]() 是抛物线
是抛物线![]() 上的一点,设
上的一点,设![]() 点的横坐标为
点的横坐标为![]() (
(![]() ),连接
),连接![]() 并延长,交抛物线
并延长,交抛物线![]() 于点
于点![]() ,交直线l于点
,交直线l于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
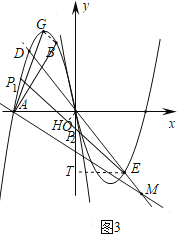
(3)如图3,在(2)的条件下,连接![]() 、
、![]() ,在直线
,在直线![]() 下方的抛物线
下方的抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ,顶点为:
,顶点为:![]() ;(2)
;(2)![]() 的值为﹣3;(3)存在,点
的值为﹣3;(3)存在,点![]() 的横坐标为:
的横坐标为:![]() 或
或![]() .
.
【解析】
(1)运用待定系数法将![]() 、
、![]() 代入
代入![]() 中,即可求得
中,即可求得![]() 和
和![]() 的值和抛物线
的值和抛物线![]() 解析式,再利用配方法将抛物线
解析式,再利用配方法将抛物线![]() 解析式化为顶点式即可求得顶点
解析式化为顶点式即可求得顶点![]() 的坐标;
的坐标;
(2)根据抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,可求得新抛物线
,可求得新抛物线![]() 的解析式,再将
的解析式,再将![]() 代入
代入![]() 中,即可求得直线
中,即可求得直线![]() 解析式,根据对称性可得点
解析式,根据对称性可得点![]() 坐标,过点
坐标,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,由
,由![]() ,即可得
,即可得![]() ,再证明
,再证明![]() ∽
∽![]() ,即可得
,即可得![]() ,建立方程求解即可;
,建立方程求解即可;
(3)连接![]() ,易证
,易证![]() 是
是![]() ,
,![]() ,可得
,可得![]() ,在
,在![]() 轴下方过点
轴下方过点![]() 作
作![]() ,在
,在![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,连接
,连接![]() 交抛物线
交抛物线![]() 于点
于点![]() ,点
,点![]() 即为所求的点;通过建立方程组求解即可.
即为所求的点;通过建立方程组求解即可.
(1)将![]() 、
、![]() 代入
代入![]() 中,得
中,得![]()
解得![]()
∴抛物线![]() 解析式为:
解析式为:![]() ,
,
配方,得:![]() ,∴顶点为:
,∴顶点为:![]() ;
;
(2)∵抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
∴新抛物线![]() 的顶点为:
的顶点为:![]() ,二次项系数为:
,二次项系数为:![]()
∴新抛物线![]() 的解析式为:
的解析式为:![]()
将![]() 代入
代入![]() 中,得
中,得![]() ,解得
,解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
∵![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由抛物线![]() 与抛物线
与抛物线![]() 关于原点对称,可得点
关于原点对称,可得点![]() 、V关于原点对称,
、V关于原点对称,
∴![]()
如图2,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]()
∴![]() ,
,
∵![]() 轴,
轴,![]() 轴
轴
∴![]()
∴![]() ∽
∽![]()
∴![]() ,即
,即![]()
∴![]()
解得:![]() ,
,![]() ,
,
∵![]()
∴![]() 的值为:﹣3;
的值为:﹣3;
(3)由(2)知:![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
如图3,连接![]() ,在
,在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() 是直角三角形,
是直角三角形,![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
在![]() 轴下方过点
轴下方过点![]() 作
作![]() ,在
,在![]() 上截取
上截取![]() ,
,
过点![]() 作
作![]() 轴于
轴于![]() ,连接
,连接![]() 交抛物线
交抛物线![]() 于点
于点![]() ,点
,点![]() 即为所求的点;
即为所求的点;
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]() ,设直线
,设直线![]() 解析式为
解析式为![]() ,
,
则![]() ,解得
,解得
∴直线![]() 解析式为
解析式为![]() ,
,
解方程组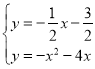 ,得
,得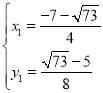 ,
,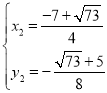 ,
,
∴点![]() 的横坐标为:
的横坐标为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
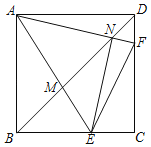
【题目】如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF、有以下结论:①AN=EN,②当AE=AF时,![]() =2﹣
=2﹣![]() ,③BE+DF=EF,④存在点E、F,使得NF>DF,其中正确的个数是( )
,③BE+DF=EF,④存在点E、F,使得NF>DF,其中正确的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一抛物线的对称轴为直线![]() ,与y轴负半轴交于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
,与y轴负半轴交于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
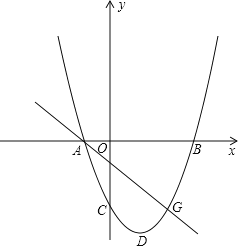
(1)求此抛物线的解析式;
(2)若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(3)若平行于x轴的直线与该抛物线交于M、N两点(其中点M在点N的右侧),在x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片ABCD折叠,使得顶点A与边CD上的动点P重合(点P不与点C、D重合),MN为折痕,点M、N分别在边BC、AD上,连结AM、MP、AP,其中,AP与MN相交于点F.⊙O过点M、C、P
(1)若∠AMP=90°,求证:BM=CP;
(2)随着点P的运动,若⊙O与AM相切于点M,又与AD相切于点H,且AB=4,求CP的长.
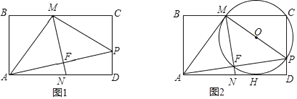
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中![]() 、
、![]() 分别表示去年、今年水费
分别表示去年、今年水费![]() (元)与用水量
(元)与用水量![]() (
(![]() )之间的关系.小雨家去年用水量为150
)之间的关系.小雨家去年用水量为150![]() ,若今年用水量与去年相同,水费将比去年多_____元.
,若今年用水量与去年相同,水费将比去年多_____元.
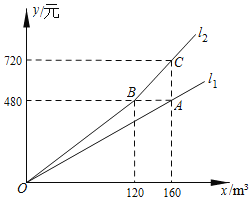
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相交于点D,且∠A=2∠DCB,连接CD.

(1)求证:AB是⊙O的切线;
(2)若BE=OE=2,求图中阴影部分的面积(结果保留![]() 和根号).
和根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com