
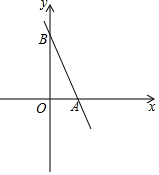
 如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.
如图,直线y=-2x+3与x轴相交于点A,与y轴相交于点B.分析 (1)把x=0,y=0分别代入函数解析式,即可求得相应的y、x的值,则易得点A、B的坐标;
(2)根据等腰三角形的判定,分两种情况讨论即可求得.
(3)根据(2)求得的AB值,结合A、B的坐标即可求得.
解答 解:(1)由x=0得:y=3,即:B(0,3).
由y=0得:-2x+3=0,解得:x=$\frac{3}{2}$,即:A($\frac{3}{2}$,0);
(2)∵A($\frac{3}{2}$,0),B(0,3).
∴AB=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,
当AB为腰长时,P的坐标为(-$\frac{3}{2}$,0)或($\frac{3+3\sqrt{5}}{2}$,0)或($\frac{3-3\sqrt{5}}{2}$,0)
当AB为底时,则AP=BP,设P(x,0)
则AP=$\frac{3}{2}$-x,
故在Rt△BOP中,
BO 2+OP2=BP 2,
即32+x2=($\frac{3}{2}$-x)2,
解得:x=-$\frac{9}{4}$,
故P′点坐标为(-$\frac{9}{4}$,0).
故P的坐标为:(-$\frac{3}{2}$,0)或($\frac{3+3\sqrt{5}}{2}$,0)或(-$\frac{9}{4}$,0)或($\frac{3-3\sqrt{5}}{2}$,0);
(3)若点P在坐标轴上,且使△ABP为以AB为腰的等腰三角形,P点的坐标为:(-$\frac{3}{2}$,0)或($\frac{3+3\sqrt{5}}{2}$,0)或($\frac{3-3\sqrt{5}}{2}$,0)或(0,$\frac{6+3\sqrt{5}}{2}$)或(0,-3)或(0,$\frac{6-3\sqrt{5}}{2}$).
点评 本题考查一次函数图象上点的坐标特征,等腰三角形的判定,两边相等的三角形是等腰三角形,以及坐标与图形的性质,分类讨论思想的运用是解题的关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
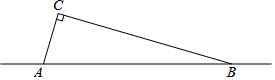 在公路AB旁有一座山,现山脚的C处需要爆破,已知点C与公路上的停靠站A的距离是700米,与公路上另一停靠站B的距离为2400米,且CA垂直于CB,为了安全起见,爆破点C周围半径680米范围内不得进入.请问在爆破时,公路AB段是否因有危险而需要暂时封锁?
在公路AB旁有一座山,现山脚的C处需要爆破,已知点C与公路上的停靠站A的距离是700米,与公路上另一停靠站B的距离为2400米,且CA垂直于CB,为了安全起见,爆破点C周围半径680米范围内不得进入.请问在爆破时,公路AB段是否因有危险而需要暂时封锁?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
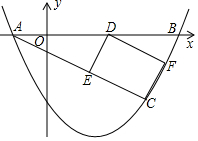 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c图象经过A(-1,0),B(4,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com