
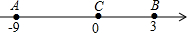 如图,数轴上有A、B两个动点,对应的数分别为-9和5,A点的运动速度为每秒1个单位,B点的运动速度为每秒3个单位.
如图,数轴上有A、B两个动点,对应的数分别为-9和5,A点的运动速度为每秒1个单位,B点的运动速度为每秒3个单位.分析 (1)设A、B两点经过t秒后重合,根据同向而行时,t秒后所表示的数相同列方程求解可得;
(2)①根据相向而行时,A、B两点的运动路程之和求得从出发到重合所需时间,即可得知点C的运动时间,继而可得点C的运动路程;
②由A、B重合求得重合点所表示的数,继而可得若此时点C从原点出发与A、B也重合时,点C的速度.
解答 解:(1)设A、B两点经过t秒后重合,
根据题意得:-9-t=5-3t,
解得:t=7,
即若A、B两点同时出发,同向而行,经过7秒后,两点重合,
故答案为:7;
(2)①设A、B两点相向而行时,x秒后两点重合,
根据题意得:x+3x=5-(-9),
解得:x=$\frac{7}{2}$,
则点C运动的路程为2×$\frac{7}{2}$=7;
②能,
由①知,$\frac{7}{2}$s后A、B重合,
重合点所表示的数为-9+$\frac{7}{2}$=-$\frac{11}{2}$,
若此时点C从原点出发,与A、B也重合,
则点C的运动速度为$\frac{11}{2}$÷$\frac{7}{2}$=$\frac{11}{7}$(单位/秒).
点评 本题主要考查一元一次方程的应用能力,熟知行程问题中相向而行和同向而行时路程之间的相等关系式解题的关键.


科目:初中数学 来源: 题型:解答题
 在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0),请按要求画图与作答:
在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0),请按要求画图与作答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若∠α+∠β=180°,则∠α是补角 | |
| B. | 若∠AOB+∠BOC=180°,则∠AOC是直角 | |
| C. | 若∠α与∠β互为补角,则∠α与∠β中必有一个为锐角,另一个角为钝角 | |
| D. | 若∠α与∠β互为余角,则∠α+∠β=90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com