
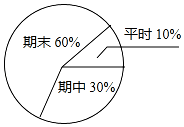
 下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题 | 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
| 成绩 | 88 | 86 | 90 | 92 | 90 | 96 |
分析 (1)依据众数定义即可求解;
(2)中位数就是大小处于中间位置的数,根据定义求解;
(3)只要运用求平均数公式,即可求出;
(4)利用加权平均数公式即可求解.
解答 解:(1)李刚同学6次成绩90分次数最多,有2次,即众数为90,
故答案为:90;
(2)成绩从大到小排列为96,92,90,90,88,86,则中位数是:$\frac{90+90}{2}$=90分,
故答案是:90分;
(3)李刚同学平时成绩的平均数是$\frac{88+86+90+92}{4}$=89分,
故答案是:89分;
(4)89×10%+90×30%+96×60%=93.5分.
答:李刚的总评分应该是93.5分.
点评 本题考查的是平均数、中位数和众数,熟练掌握平均数、中位数和众数的定义和计算公式是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{2-3x≥2x-8}\\{\frac{2-x}{3}-2<\frac{x-1}{2}}\end{array}\right.$,把它的解集在数轴上表示出来,并写出这个不等式组的整数解.
解不等式组:$\left\{\begin{array}{l}{2-3x≥2x-8}\\{\frac{2-x}{3}-2<\frac{x-1}{2}}\end{array}\right.$,把它的解集在数轴上表示出来,并写出这个不等式组的整数解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com