
【题目】如图,在等腰三角形![]() 中,
中,![]() 是
是![]() 上一动点,点
上一动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
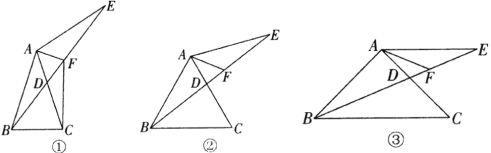
(1)如图①,连接![]() ,求证:
,求证: ![]() ;
;
(2)如图②,当![]() 时,求证:
时,求证: ![]() ;
;
(3)如图③,当![]() 时,若
时,若![]() 平分
平分![]() ,求证:
,求证: ![]() .
.
【答案】见解析
【解析】
(1)证△EAF≌△CAF,推出EF=CF,∠E=∠ACF,根据等腰三角形性质推出∠E=∠ABF,即可得出答案;
(2)在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等边三角形,推出MF=AF,即可得出答案;
(3)连接CF,延长BA、CF交N,证△BFC≌△BFN,推出CN=2CF=2EF,证△BAD≌△CAN,推出BD=CN,即可得出答案.
(1)∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
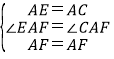 ,
,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF.
(2)连接CF,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在FB上截取BM=CF,连接AM,
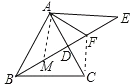
在△ABM和△ACF中,
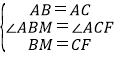 ,
,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形,
∴AF=AM=MF,
∴AF+EF=BM+MF=FB,
即AF+EF=FB;
(3)连接CF,延长BA、CF交N,
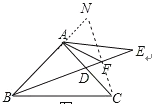
∵∠ABC=45°,BD平分∠ABC,AB=AC,
∴∠ABF=∠CBF=22.5°,∠ACB=45°,∠BAC=180°45°45°=90°,
∴∠ACF=∠ABF=22.5°,
∴∠BFC=180°22.5°45°22.5°=90°,
∴∠BFN=∠BFC=90°,
在△BFN和△BFC中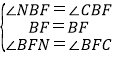 ,
,
∴△BFN≌△BFC(ASA),
∴CF=FN,
即CN=2CF=2EF,
∵∠BAC=90°,
∴∠NAC=∠BAD=90°,
在△BAD和△CAN中,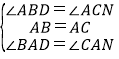 ,
,
∴△BAD≌△CAN(ASA),
由(2)得CF=EF,
∴BD=CN=2CF=2EF.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
A.9:4
B.3:2
C.16:9
D.4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
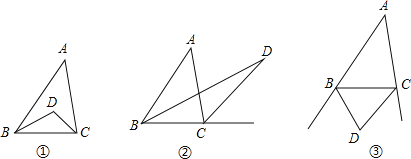
【题目】如图①,△ABC中,DC,BD分别是∠ACB和∠ABC的平分线,且∠A=α
(1)用含α的代数式表示∠CDB;
(2)若把图①中∠ACB的平分线DC改为∠ACB的外角的平分线(如图②),怎样用含α的代数式表示∠CDB.
(3)若把图①中“DC,DB分别是∠ACB和∠ABC的平分线”改成“DC,BD分别是∠ACB和∠ABC的外角的平分线”,(如图③),怎样用含α的代数式表示∠CDB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分). 
(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O是△ABC的外接圆,AB是直径,过 ![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP; 
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG; 
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ![]() ,求AC的长.
,求AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人沿一条直路行走,此人离出发地的距离![]() 千米
千米![]() 与行走时间
与行走时间![]() 分钟
分钟![]() 的函数关系如图所示,请根据图象提供的信息回答下列问题:
的函数关系如图所示,请根据图象提供的信息回答下列问题:
![]() 此人离开出发地最远距离是______ 千米;
此人离开出发地最远距离是______ 千米;
![]() 此人在这次行走过程中,停留所用的时间为______ 分钟;
此人在这次行走过程中,停留所用的时间为______ 分钟;
![]() 由图中线段OA可知,此人在这段时间内行走的速度是每小时______ 千米;
由图中线段OA可知,此人在这段时间内行走的速度是每小时______ 千米;
![]() 此人在120分钟内共走了______ 千米.
此人在120分钟内共走了______ 千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
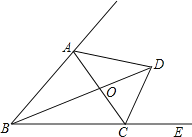
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是__________.(填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com