
分析 根据题意可以求得半径为2的圆内接正三角形,正四边形,正六边形的边心距,从而可以求得它们的比值.
解答 解:由题意可得,
正三角形的边心距是:2×sin30°=2×$\frac{1}{2}$=1,
正四边形的边心距是:2×sin45°=2×$\frac{\sqrt{2}}{2}=\sqrt{2}$,
正六边形的边心距是:2×sin60°=2×$\frac{\sqrt{3}}{2}=\sqrt{3}$,
∴半径为2的圆内接正三角形,正四边形,正六边形的边心距之比为:1:$\sqrt{2}$:$\sqrt{3}$,
故答案为:1:$\sqrt{2}$:$\sqrt{3}$.
点评 本题考查正多边形和圆,解答本题的关键是明确题意,求出相应的图形的边心距.


科目:初中数学 来源: 题型:解答题
| x | 4 | 5 | 6 | 7 |
| y | 550 | 500 | 450 | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
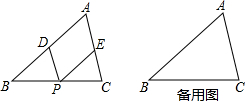 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
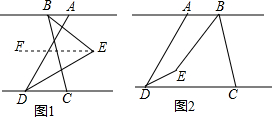
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
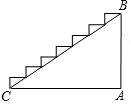 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )| A. | 3.5sin29°米 | B. | 3.5cos29°米 | C. | 3.5tan29°米 | D. | $\frac{3.5}{cos29°}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 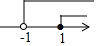 | B. |  | C. | 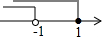 | D. | 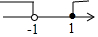 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
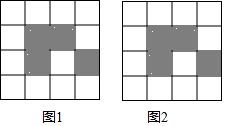 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com