
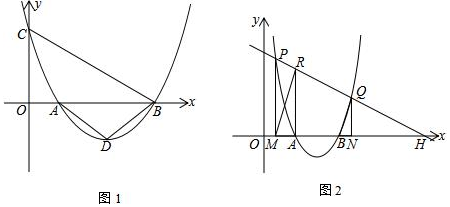
分析 (1)先设抛物线与x轴交点A、B两点的坐标:设A(x1,0),B(x2,0),由根与系数的关系得:x1•x2=c,证明△AOC∽△COB,得OC2=OA•OB,则c2=x1•x2=c,解方程可得c的值;
(2)根据抛物线的对称性得:AD=BD,由等腰三角形性质和三角形内角和可知:∠DAB=30°,根据特殊的三角函数得:tan30°=$\frac{DE}{AE}$=$\frac{\sqrt{3}}{3}$,则AE=$\sqrt{3}$DE,列式可得结论;
(3)如图2,设A(x1,0),B(x2,0),由根与系数关系得:x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,设P(x3,kx3+m),Q(x4,kx4+m),则ax2+bx+c=kx+m,同理得:x3+x4=-$\frac{b-k}{a}$,x3x4=$\frac{c-m}{a}$,
根据tan∠RMA-tan∠QBN列式,计算(kx1+m)(x4-x2)-(kx4+m)(x1-x3)=0,则∠RMA=∠QBN,得平行和相似,由相似三角形的性质:相似三角形面积的比等于对应边的平方列式可得结论.
解答 解:(1)设A(x1,0),B(x2,0),
当a=1时,抛物线的解析式为:y=x2+bx+c,
当y=0时,x2+bx+c=0,
∴x1•x2=c,
∵∠ACO=∠OBC,∠AOC=∠AOC,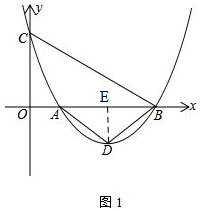
∴△AOC∽△COB,
∴$\frac{OA}{CO}=\frac{OC}{OB}$,
∴OC2=OA•OB,
∴c2=x1•x2=c,
c(c-1)=0,
c1=0(舍),c2=1;
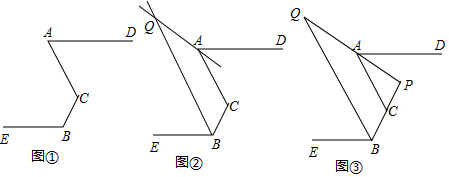
(2)如图1,∵∠ADB=120°,AD=BD,
∴∠DAB=30°,
过D作DE⊥AB于E,
∴tan30°=$\frac{DE}{AE}$=$\frac{\sqrt{3}}{3}$,
∴AE=$\sqrt{3}$DE,
即:$\frac{{x}_{2}-{x}_{1}}{2}$=$\sqrt{3}$DE,
∵${x}_{1}=\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$,${x}_{2}=\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,
∴x2-x1=$\frac{-b+\sqrt{{b}^{2}-4ac}+b+\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{\sqrt{{b}^{2}-4ac}}{a}$,
∴$\frac{\sqrt{{b}^{2}-4ac}}{2a}$=-$\sqrt{3}$$•\frac{4ac-{b}^{2}}{4a}$,
b2-4ac=$\frac{4}{3}$;
(3)如图2,设A(x1,0),B(x2,0),
当y=0时,y=ax2+bx+c=0,
∴x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,
设P(x3,kx3+m),Q(x4,kx4+m),
ax2+bx+c=kx+m,
ax2+(bx-k)x+c-m=0,
x3+x4=-$\frac{b-k}{a}$,x3x4=$\frac{c-m}{a}$,
tan∠RMA-tan∠QBN=$\frac{k{x}_{1}+m}{{x}_{1}-{x}_{3}}$-$\frac{k{x}_{4}+m}{{x}_{4}-{x}_{2}}$=$\frac{(k{x}_{1}+m)({x}_{4}-{x}_{2})-(k{x}_{4}+m)({x}_{1}-{x}_{3})}{({x}_{1}-{x}_{3})({x}_{4}-{x}_{2})}$,
∵(kx1+m)(x4-x2)-(kx4+m)(x1-x3)=k(x4x3-x1x2)+m(x4+x3-x1-x2)=k($\frac{c-m}{a}$-$\frac{c}{a}$)+m($\frac{k-b}{a}$+$\frac{b}{a}$)=0,
∴∠RMA=∠QBN,
∴PM∥QB,
∴△RMA∽△QBN,
∴$\frac{RM}{QB}$=$\sqrt{\frac{{S}_{△RMA}}{{S}_{△QBN}}}$=2,
∵RM∥QB,
∴$\frac{BH}{MH}=\frac{BQ}{RM}$=$\frac{1}{2}$.
点评 本题是二次函数的综合题,考查了抛物线与一元二次方程的关系、根与系数的关系、函数的交点、三角函数、三角形相似的性质和判定,熟练掌握一元二次方程根与系数的关系是关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
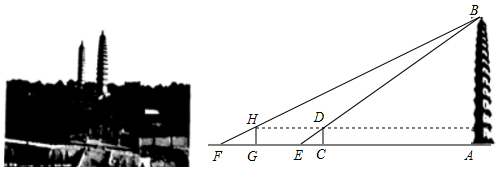
 如图,已知直线EF交x轴于点E(18,0),交y轴于点F,∠FEO=30°,C、D为EF上两点,且两点的横坐标分别为12和6;DA⊥y轴于点A,CB⊥y轴于点B,CQ⊥x轴于点Q.
如图,已知直线EF交x轴于点E(18,0),交y轴于点F,∠FEO=30°,C、D为EF上两点,且两点的横坐标分别为12和6;DA⊥y轴于点A,CB⊥y轴于点B,CQ⊥x轴于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
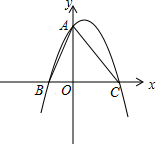 如图,在平面直角坐标系中,二次函数y=-x2+x+6的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
如图,在平面直角坐标系中,二次函数y=-x2+x+6的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com