练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    材料：① 1的任何次幂都为1；② -1的奇数次幂为-1；③ -1的偶数次幂也为1；④任何不等于零的数的零次幂都为1；请问当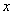为何值时，代数式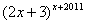的值为1.


    解：①当2x+3=1时，x=-1；（2分）

    ②当2x+3=-1时，x=-2，但此时x+2011=2009是奇数，所以x≠-2；（2分）

    ③当x+2011=0时，x=-2011此时2x+3=-4019≠0；（2分）

    综上所述：当x=-1或x=-2011时，代数式（2x+3）x+2011的值为1．

    故答案为：x=-1或x=-2011．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知(10x31)(13x17)(13x17)(3x23)可因式分解成(axb)(7xc)，其中a、b、c均为整数，求abc的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，则=          

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直线与半径的圆O相交，且点O到直线的距离为6，则的取值范围是（    ）

    A、          B、           C、         D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若某直角三角形的一个锐角的正切值为，则这个直角三角形中另一个锐角的余弦值为         

    查看答案和解析>>

    科目：初中数学 来源： 题型：


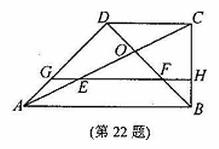
    在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，对角线AC与BD相交于

    点O，线段OA，OB的中点分别为E，F。 （1）求证：△FOE≌△DOC；

    （2）求tan∠BOC的值；  （3）设△AGE, △EFO,△BFH的面积分别为S1，S2, S3,

    求S1： S2： S3 的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （    ）

    A．     B．0<    C．      D．0<

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，抛物线y＝nx2－11nx＋24n (n＜0) 与x轴交于B、C两点（点B在点C的左侧），抛物线上另有一点A在第一象限内，且∠BAC＝90°．

    （1）填空：点B的坐标为（_        ），点C的坐标为（_        ）；

    （2）连接OA，若△OAC为等腰三角形．

    ①求此时抛物线的解析式；

    ②如图2，将△OAC沿x轴翻折后得△ODC，点M为①中所求的抛物线上点A与点C两点之间一动点，且点M的横坐标为m，过动点M作垂直于x轴的直线l与CD交于点N，试探究：当m为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．

     


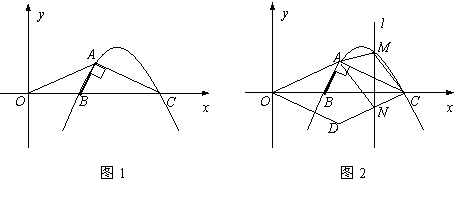    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：，其中a，b满足.

    查看答案和解析>>

    同步练习册答案