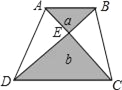
【题目】如图，梯形ABCD中，AB∥CD，两条对角线交于点E．已知△ABE的面积是a，△CDE的面积是b，则梯形ABCD的面积是（ ）
A. a2+b2 B. 
（a+b） C. 
D. （a+b）2
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】下列说法：①
必是负数；②绝对值最小的数是0；③在数轴上，原点两旁的两个点表示的数必互为相反数；④在数轴上，左边的点比右边的点所表示的数大，其中正确的有（ ）
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：小明热爱数学，在课外书上看到了一个有趣的定理——“中线长定理”：三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍．如图1，在△ABC中，点D为BC的中点，根据“中线长定理”，可得：
AB2＋AC2＝2AD2＋2BD2．
小明尝试对它进行证明，部分过程如下：
解：过点A作AE⊥BC于点E，如图2，在Rt△ABE中，AB2＝AE2＋BE2，
同理可得：AC2＝AE2＋CE2，AD2＝AE2＋DE2，
为证明的方便，不妨设BD＝CD＝x，DE＝y，
∴AB2＋AC2＝AE2＋BE2＋AE2＋CE2＝……
（1）请你完成小明剩余的证明过程；
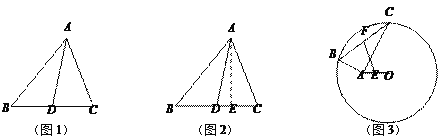
理解运用：
（2） ① 在△ABC中，点D为BC的中点，AB＝6，AC＝4，BC＝8，则AD＝_______；
② 如图3，⊙O的半径为6，点A在圆内，且OA＝2
，点B和点C在⊙O上，且∠BAC＝90°，点E、F分别为AO、BC的中点，则EF的长为________；
拓展延伸：
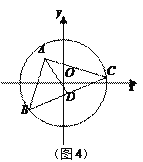
（3）小明解决上述问题后，联想到《能力训练》上的题目：如图4，已知⊙O的半径为5
，以A(3，4)为直角顶点的△ABC的另两个顶点B，C都在⊙O上，D为BC的中点，求AD长的最大值．请你利用上面的方法和结论，求出AD长的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB＝20，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．
（1）数轴上点B表示的数是 ，点P表示的数是 ；（用含t的代数式表示）
（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时，P、Q之间的距离恰好等于2；
（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，直接写出多少秒时，P、Q之间的距离恰好等于2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店第一次购进相同铅笔1000支，第二次又购进同种铅笔，购进数量是第一次的
，这次每支铅笔的进价比第一次进价高0.2元，第二次购进铅笔比第一次少花300元．
（1）求第一次每支铅笔的进价是多少元？
（2）第一次购进铅笔在第一次进价的基础上加价50%出售；第二次购进的铅笔以每支1.5元的价格出售，出售一部分后又在每支1.5元的基础上打八折出售；两次购进的铅笔全部销售完毕后总获利为560元，问第二次购进的铅笔出售多少支后打八折出售？
查看答案和解析>>
科目：初中数学 来源： 题型：
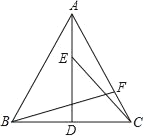
【题目】如图，AD为等边△ABC的高，E、F分别为线段AD、AC上的动点，且AE＝CF，当BF+CE取得最小值时，∠AFB＝（ ）
A. 112.5°B. 105°C. 90°D. 82.5°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】轮胎的直径是否符合标准，是判断轮胎质量的好与差的重要依据之一．东风轮胎厂某批轮胎的标准直径是
，质量检验员从这批产品中抽取10个轮胎进行检查，超过标准直径的毫米数记为正，不足的毫米数记为负，检查记录如下(单位：
)：
（1）若与标准直径比较相差不超过
的为合格品，请用所学的数学知识说明第几号轮胎不合格？不合格轮胎的实际直径是多少毫米？
（2）若与标准直径比较相差不超过的为合格品，请根据抽查的结果估算一下这批轮胎的合格率大约是多少？
（3）求这10个轮胎的平均直径(精确到
)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法：
①连接两点间的线段叫这两点的距离；
②木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；
③若
三点在同一直线上，且
，则
是线段
的中点；
④若
，则有
．
其中一定正确的是_________(把你认为正确结论的序号都填上) ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：
收费项目 | 收费标准 |
3公里以内收费 | 13元 |
基本单价 | 2.3元/公里 |
…… | …… |
备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。
小明首先简化模型，从简单情形开始研究：①只考虑白天正常行驶（无低速和等候）；②行驶路程3公里以上时，计价器每500米计价1次，且每1公里中前500米计价1.2元，后500米计价1.1元.
下面是小明的探究过程，请补充完整：
记一次运营出租车行驶的里程数为
（单位：公里），相应的实付车费为
（单位：元）.
（1）下表是y随x的变化情况
行驶里程数x | 0 | 0＜x＜3.5 | 3.5≤x＜4 | 4≤x＜4.5 | 4.5≤x＜5 | 5≤x＜5.5 | … |
实付车费y | 0 | 13 | 14 | 15 | … |
（2）在平面直角坐标系
中，画出当
时随变化的函数图象；
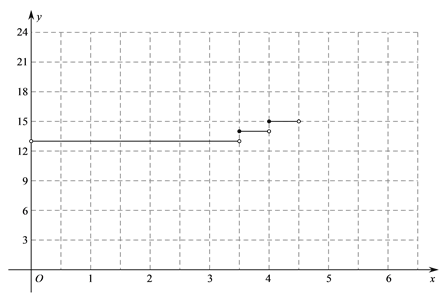
（3）一次运营行驶公里（
）的平均单价记为
（单位：元/公里），其中
.
①当
和
时，平均单价依次为
，则的大小关系是____________；（用“＜”连接）
②若一次运营行驶公里的平均单价不大于行驶任意
（
）公里的平均单价
，则称这次行驶的里程数为幸运里程数.请在上图中轴上表示出
（不包括端点）之间的幸运里程数的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
