练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    二次函数图像的最低点坐标是      ．
    （0，-3）

    试题分析：由二次函数图像可知，该抛物线的开口向上，所以最低点在对称轴上，因对称轴为y轴，所以当x=0，y=-3，所以最低点坐标是（0，-3）.
    点评：该题是常考题，主要考查学生对二次函数解析式和抛物线图像理解，建议学生通过画图直观理解问题。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
    小丽：如果以10元/千克的价格销售，那么每天可售出300千克．
    小强：如果每千克的利润为3元，那么每天可售出250千克．
    小红：如果以13元/千克的价格销售，那么每天可获取利润750元．
    【利润=（销售价-进价）销售量】
    （1）请根据他们的对话填写下表：
    销售单价x（元/kg）
    		10
    		11
    		13
    销售量y（kg）
    		 
    		 
    		 
    （2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系．并求y（千克）与x（元）（x＞0）的函数关系式；
    （3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式．当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知抛物线 经过A（2，0）． 设顶点为点P，与x轴的另一交点为点B．

    （1）求b的值和点P、B的坐标；
    （2）如图，在直线上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；
    （3）在轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在,试举例验证你的猜想；如果不存在，试说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

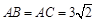    如图，已知在△ABC中，∠A = 90°，，经过这个三角形重心的直线DE // BC，分别交边AB、AC于点D和点E，P是线段DE上的一个动点，过点P分别作PM⊥BC，PF⊥AB，PG⊥AC，垂足分别为点M、F、G．设BM = x，四边形AFPG的面积为y．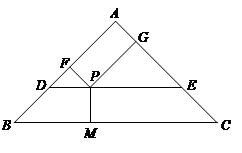

    （1）求PM的长；
    （2）求y关于x的函数解析式，并写出它的定义域；
    （3）联结MF、MG，当△PMF与△PMG相似时，求BM的长．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

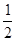    如图，抛物线y=x2+bx－2与x轴交于A、B两点，与y 轴交于C点，且A（一1，0）．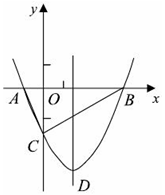

    （1）求抛物线的解析式及顶点D的坐标；
    （2）若将上述抛物线先向下平移3个单位，再向右平移2个单位，请直接写出平移后的抛物线的解析式.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

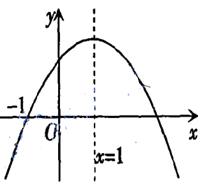
    已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图，则下列结论中正确的是
    A．ac>0 　　　　　　　　　　　B．当x>1时，y随x的增大而增大
    C．2a＋b＝1 　　　　　　　　　D．方程ax2＋bx＋c＝0有一个根是x＝3

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图①是矩形包书纸的示意图，虚线是折痕，四个角均为大小相同的正方形，正方形的边长为折叠进去的宽度.

    （1）现有一本书长为25cm，宽为20cm，厚度是2cm，如果按照如图①的包书方式，并且折叠进去的宽度是3cm，则需要书包纸的长和宽分别为多少？（请直接写出答案）.
    （2）已知数学课本长为26 cm，宽为18.5cm，厚为1cm，小明用一张面积为1260cm2的矩形书包纸按如图①包好了这本书，求折进去的宽度.
    （3）如图②，矩形ABCD是一张一个角(△AEF)被污损的书包纸，已知AB=30，BC=50，AE=12，AF=16，要使用没有污损的部分包一本长为19，宽为16，厚为6的字典，小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典. 设PM=x，矩形PGCH的面积为y，当x取何值时y最大？并由此判断小红的想法是否可行.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

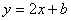    已知：如图，直线交x轴于点B，交y轴于点C，点A为x轴正半轴上一点，AO=CO，△ABC的面积为12．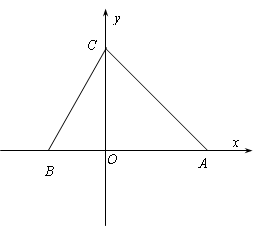

    （1）求b的值；
    （2）若点P是线段AB中垂线上的点，是否存在这样的点P，使△PBC成为直角三角形．若存在，试直接写出所有符合条件的点P的坐标；若不存在，试说明理由；
    （3）点Q为线段AB上一个动点（点Q与点A、B不重合），QE∥AC，交BC于点E，以QE为边，在点B的异侧作正方形QEFG．设AQ=m，△ABC与正方形QEFG的重叠部分的面积为S，试求S与m之间的函数关系式，并写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

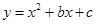    二次函数的图象如图所示，其顶点坐标为M(1,-4)．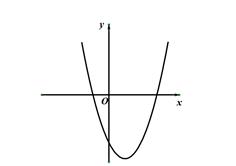

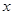    （1）求二次函数的解析式；
    （2）将二次函数的图象在轴下方的部分沿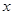轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线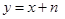与这个新图象有两个公共点时，求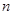的取值范围．

    查看答案和解析>>

    同步练习册答案