
【题目】在一个不透明的口袋中放入![]() 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为
个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为![]() 、
、![]() 、
、![]() 克,已知随机的摸出一个鸡蛋,摸到
克,已知随机的摸出一个鸡蛋,摸到![]() 克和
克和![]() 克的鸡蛋的概率是相等的.
克的鸡蛋的概率是相等的.
(1)求这四个鸡蛋质量的众数和中位数
(2)小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为![]() 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是
克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是![]() 克的鸡蛋的概率?
克的鸡蛋的概率?
【答案】(1)因此鸡蛋质量的众数为![]() ,中位数也是
,中位数也是![]() .(2)①
.(2)①![]() ;②
;②![]()
【解析】
(1)因为![]() 个鸡蛋有三个质量数,所以必然有两个鸡蛋的质量是相等的,又根据摸到
个鸡蛋有三个质量数,所以必然有两个鸡蛋的质量是相等的,又根据摸到![]() 克的鸡蛋和
克的鸡蛋和![]() 克的鸡蛋概率相等,从而可得答案,
克的鸡蛋概率相等,从而可得答案,
(2)①若小明分别拿走的是不同的鸡蛋,分析剩下的鸡蛋,可得到答案,
②利用树状图得到两次拿走50克鸡蛋的机会,从而可得答案.
解(1)因为![]() 个鸡蛋有三个质量数,所以必然有两个鸡蛋的质量是相等的,所以四个鸡蛋的质量可能为
个鸡蛋有三个质量数,所以必然有两个鸡蛋的质量是相等的,所以四个鸡蛋的质量可能为![]() 、
、![]() 、
、![]() 、
、![]() ;
;![]() 、
、![]() 、
、![]() 、
、![]() ;
;![]() 、
、![]() 、
、![]() 、
、![]() .又根据摸到
.又根据摸到![]() 克的鸡蛋和
克的鸡蛋和![]() 克的鸡蛋概率相等,
克的鸡蛋概率相等,
我们从前面数据分析可知,摸到鸡蛋的的概率分别是![]() ,
,![]() ,
,![]() ,
,
所以我们知道四个鸡蛋的质量数为![]() 、
、![]() 、
、![]() 、
、![]() ;
;
因此鸡蛋质量的众数为![]() ,中位数也是
,中位数也是![]() .
.
(2)①若小明拿走的是49,剩下的是![]() ,
,![]() ,
,![]() ,此时中位数是50,
,此时中位数是50,
若小明拿走的是50,剩下的是49、![]() ,
,![]() ,此时中位数是50,
,此时中位数是50,
若小明拿走的是51,剩下的是49,![]() ,
,![]() ,此时中位数是50,
,此时中位数是50,
所以小明拿走一个鸡蛋,不管小明拿走的鸡蛋质量是多少,剩下鸡蛋的中位数都是![]() ;
;
②画树状图如下:
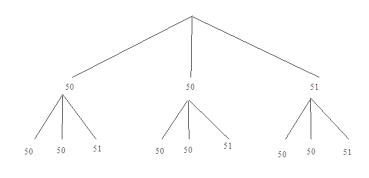
共有![]() 种情况:
种情况:![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() .其中两次拿到
.其中两次拿到![]() 克的情况有四种,所以两次都拿到
克的情况有四种,所以两次都拿到![]() 克鸡蛋的概率为
克鸡蛋的概率为![]()


科目:初中数学 来源: 题型:
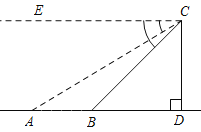
【题目】如图,直升飞机在大桥AB上方C点处测得A,B两点的俯角分别为45°和31°.若飞机此时飞行高度CD为1205m,且点A,B,D在同一条直线上,求大桥AB的长.(精确到1m)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
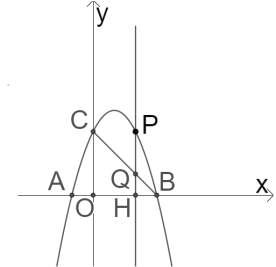
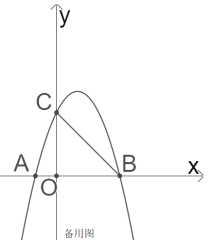
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C(0,3),点P是抛物线在第一象限上的一点,过点P作PH⊥x轴,垂足为H,交线段BC于点Q.
(1)求抛物线对应的函数表达式;
(2)当PQ=2QH时,求点P的坐标;
(3)当PH最大时,连接AP,AP与BC交于点D,点F是第一象限内一点,且∠AFC=45°,点G在抛物线上,直线FG、FC分别与直线PH交于点M、N.当三角形ABD相似三角形FMN时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,
上,![]() ,
,![]() ,连接
,连接![]() ,线段
,线段![]() 绕点
绕点![]() 旋转
旋转![]() ,得到线段
,得到线段![]() ,以线段
,以线段![]() 为直径做
为直径做![]() .
.
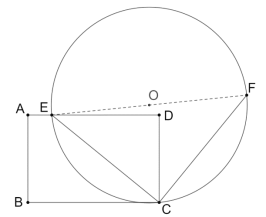

(1)请说明点![]() 一定在
一定在![]() 上的理由,
上的理由,
(2)①点![]() 在
在![]() 上,
上,![]() 为
为![]() 的直径,求证:点
的直径,求证:点![]() 到
到![]() 的距离等于线段
的距离等于线段![]() 的长.
的长.
②当![]() 面积取得最大值时,求
面积取得最大值时,求![]() 半径的长.
半径的长.
(3)当![]() 与矩形
与矩形![]() 的边相切时,计算扇形
的边相切时,计算扇形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 为线段
为线段![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),连接
重合),连接![]() ,作
,作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
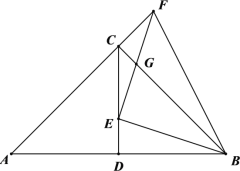
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
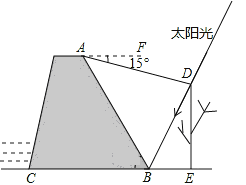
【题目】星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知斜坡AB的坡度为![]() ,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:
,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com