
【题目】在△ABC中,∠ACB=90AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当MN绕点C旋转到图1的位置时,请你探究线段DE、AD、BE之间的数量关系(直接写出结论,不要求写出证明过程);
(2)当MN绕点C旋转到图2的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想,并加以证明;
(3)当MN绕点C旋转到图3的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想,并加以证明。

【答案】见解析
【解析】【试题分析】
(1)思路先证明△ACD≌△CBE.(AAS)再利用全等三角形的性质对应边相等,得AD=CE,CD=BE,则DE=AD+BE.
(2)思路同(1),这是第(1)题的变式,实质问题没变。
(3)这是(1)问题的变式,实质问题没变。
【试题解析】
(1)DE=AD+BE.
(2)猜想:(1)中得到的结论发生了变化。
证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°.
∴∠BCE+∠CBE=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°.
∴∠ACD=∠CBE.
∵AC=CB,
∴△ACD≌△CBE.
∴AD=CE,CD=BE.
∵DE=CECD,
∴DE=ADBE.
(3)如图3,
猜想:(1)中得到的结论发生了变化。
证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°.
∴∠BCE+∠CBE=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°.
∴∠ACD=∠CBE.
∵AC=CB,
∴△ACD≌△CBE.
∴AD=CE,CD=BE.
∵DE=CDCE,
∴DE=BEAD.


科目:初中数学 来源: 题型:
【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC( )
A. 三条角平分线的交点 B. 三条中线的交点
C. 三条高的交点 D. 三边垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数x满足﹣5≤x≤5,y1=x+1,y2=2x+4,对于任意一个x,m都取y1、y2中的最小值,则m的最大值是( )
A. ﹣4 B. ﹣6 C. 14 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代民间流传着这也一道数学题“只闻隔壁客分银,不知人数不知银,四两一分多四两,半斤一分少半斤.借问各位能算者,多少客人多少银?其大意是:有客人在分银子,若每人分四两,则多出四两,若每人分半斤,则少半斤.问有多少客人?多少银子?(注:古代旧制:半斤=8两),试用列方程(组)解应用题的方法求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
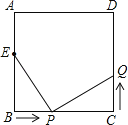
(1)如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com