
分析 先化简分式,再把x=2代入求解即可.
解答 解:($\frac{{x}^{2}+2x-3}{9-{x}^{2}}$)3•($\frac{3-x}{1-x}$)2
=[$\frac{(x+3)(x-1)}{(3+x)(3-x)}$]3•$\frac{(3-x)^{2}}{(1-x)^{2}}$,
=$\frac{(x+3)^{3}(x-1)^{3}}{(3+x)^{3}(3-x)^{3}}$•$\frac{(3-x)^{2}}{(1-x)^{2}}$,
=$\frac{x-1}{3-x}$,
当x=2时,原式=$\frac{2-1}{3-2}$=1.
点评 本题主要考查了分式的化简求值,解题的关键是正确的化简分式.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
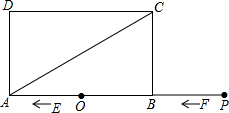 如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
如图,矩形ABCD中,AB=6,BC=$2\sqrt{3}$,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com