
分析 (1)利用求根公式找出x1,x2,将其相加(相乘)整理后即可得出结论;
(2)根据根与系数的关系即可得出m+n=-1、mn=-1,将$\frac{n}{m}$+$\frac{m}{n}$边形为$\frac{(m+n)^{2}-2mn}{mn}$,再代入数据即可得出结论.
解答 (1)证明:∵x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,
∴x1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,x2=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$,
∴x1+x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-2b}{2a}$=-$\frac{b}{a}$.
x1x2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$•$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{(-b)^{2}-({b}^{2}-4ac)}{4{a}^{2}}$=$\frac{{b}^{2}-{b}^{2}+4ac}{4{a}^{2}}$=$\frac{4ac}{4{a}^{2}}$=$\frac{c}{a}$.
(2)解:∵一元二次方程x2+x-1=0的两根为m,n,
∴m+n=-1,mn=-1,
∴$\frac{n}{m}$+$\frac{m}{n}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{{1}^{2}-2×(-1)}{-1}$=-3.
点评 本题考查了根与系数的关系以及公式法解一元二次方程,解题的关键是:(1)利用公式法求出x1,x2的值;(2)根据根与系数的关系找出m+n=-1、mn=-1.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:解答题
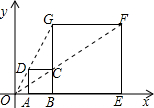 如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上.
如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
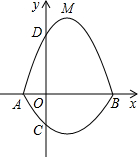 如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com