
| A. | 28 | B. | 26 | C. | 18 | D. | 35 |
分析 作辅助线“连接AO,DO,作OM⊥CD于点M,作ON⊥AB于点N”构造矩形ENOM,然后利用勾股定理和垂径定理推知,OM2=DO2-DM2=4-($\frac{AB}{2}$)2、ON2=OA2-AN2=4-($\frac{DC}{2}$)2,所以OM2+ON2=4-($\frac{AB}{2}$)2+4-($\frac{DC}{2}$)2=1,由此解得AB2+CD2=28.
解答 解:连接AO,DO,作OM⊥CD于点M,作ON⊥AB于点N,
∵DC⊥AB,OM⊥DC,ON⊥AB,
∴四边形OMEN为矩形;
∵OM2+ME2=OE2(勾股定理),
又∵ME2=ON2
∴OM2+ON2=OE2;
∵OM2=DO2-DM2=4-($\frac{DC}{2}$)2;
又∵ON2=OA2-AN2=4-($\frac{AB}{2}$)2,
∴OM2+ON2=4-($\frac{AB}{2}$)2+4-($\frac{DC}{2}$)2=1,
∴AB2+CD2=28.
故选A.
点评 本题主要考查了的是垂径定理和勾股定理.解得该题的关键是通过作辅助线构建矩形OMEN,利用勾股定理、矩形的性质以及垂径定理将 AB2+CD2联系在同一个等式中,然后根据代数知识求解.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ABC中,∠C=90°,tanB=$\frac{1}{4}$,AD是BC边上的中线,则sin∠BAD=$\frac{2\sqrt{85}}{85}$.
如图,Rt△ABC中,∠C=90°,tanB=$\frac{1}{4}$,AD是BC边上的中线,则sin∠BAD=$\frac{2\sqrt{85}}{85}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -1 | 1 | 2 | … |
| y | … | m | 2 | n | … |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )
如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )| A. | 6 | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
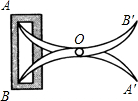 如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..
如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com