
”¾ĢāÄæ”æČēĶ¼1£¬ŹĒŅ»½ØÖžĪļŌģŠĶµÄׯ½ŲĆę£¬ĒśĻß![]() ŹĒÅ×ĪļĻßµÄŅ»²æ·Ö£¬øĆÅ×ĪļĻßæŖæŚĻņÓŅ”¢¶Ō³ĘÖįÕżŗĆŹĒĖ®Ę½Ļß
ŹĒÅ×ĪļĻßµÄŅ»²æ·Ö£¬øĆÅ×ĪļĻßæŖæŚĻņÓŅ”¢¶Ō³ĘÖįÕżŗĆŹĒĖ®Ę½Ļß![]() £¬
£¬![]() £¬
£¬![]() ŹĒÓėĖ®Ę½Ļß
ŹĒÓėĖ®Ę½Ļß![]() “¹Ö±µÄĮ½øłÖ§Öł£¬
“¹Ö±µÄĮ½øłÖ§Öł£¬![]() Ć×£¬
Ć×£¬![]() Ć×£¬
Ć×£¬![]() Ć×.
Ć×.
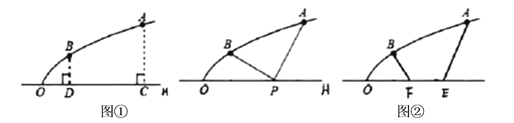
£Ø1£©ČēĶ¼1£¬ĪŖĮĖ°²Č«ĆĄ¹Ū£¬×¼±ø²š³żÖ§Öł![]() ”¢
”¢![]() £¬ŌŚĖ®Ę½Ļß
£¬ŌŚĖ®Ę½Ļß![]() ÉĻĮķÕŅŅ»µć
ÉĻĮķÕŅŅ»µć![]() ×÷ĪŖµŲĆęÉĻµÄÖ§³Åµć£¬ÓĆ¹Ģ¶Ø²ÄĮĻĮ¬½Ó
×÷ĪŖµŲĆęÉĻµÄÖ§³Åµć£¬ÓĆ¹Ģ¶Ø²ÄĮĻĮ¬½Ó![]() ”¢
”¢![]() £¬¶ŌÅ×ĪļĻßŌģŠĶ½ųŠŠÖ§³Å¼Ó¹Ģ£¬ÓĆĮĻ×īŹ”Ź±µć
£¬¶ŌÅ×ĪļĻßŌģŠĶ½ųŠŠÖ§³Å¼Ó¹Ģ£¬ÓĆĮĻ×īŹ”Ź±µć![]() £¬
£¬![]() Ö®¼äµÄ¾ąĄėŹĒ_________.
Ö®¼äµÄ¾ąĄėŹĒ_________.
£Ø2£©ČēĶ¼2£¬ŌŚĖ®Ę½Ļß![]() ÉĻŌöĢķŅ»ÕÅ
ÉĻŌöĢķŅ»ÕÅ![]() Ć׳¤µÄŅĪ×Ó
Ć׳¤µÄŅĪ×Ó![]() £Ø
£Ø![]() ŌŚ
ŌŚ![]() ÓŅ²ą£©£¬ÓĆ¹Ģ¶Ø²ÄĮĻĮ¬½Ó
ÓŅ²ą£©£¬ÓĆ¹Ģ¶Ø²ÄĮĻĮ¬½Ó![]() ”¢
”¢![]() £¬¶ŌÅ×ĪļĻßŌģŠĶ½ųŠŠÖ§³Å¼Ó¹Ģ£¬ÓĆĮĻ×īŹ”Ź±µć
£¬¶ŌÅ×ĪļĻßŌģŠĶ½ųŠŠÖ§³Å¼Ó¹Ģ£¬ÓĆĮĻ×īŹ”Ź±µć![]() £¬
£¬![]() Ö®¼äµÄ¾ąĄėŹĒ_______________.
Ö®¼äµÄ¾ąĄėŹĒ_______________.
”¾“š°ø”æ![]()
![]()
”¾½āĪö”æ
£Ø1£©ŅŌµćOĪŖŌµć£¬OCĖłŌŚÖ±ĻßĪŖyÖį£¬“¹Ö±ÓŚOCµÄÖ±ĻßĪŖxÖį½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£¬ĄūÓĆ“ż¶ØĻµŹż·ØČ·¶Ø¶ž“ĪŗÆŹżµÄ½āĪöŹ½ŗóŃÓ³¤BDµ½MŹ¹MD=BD£¬Į¬½ÓAM½»OCÓŚµćP£¬ŌņµćP¼“ĪŖĖłĒó£»ĄūÓĆ“ż¶ØĻµŹż·ØČ·¶ØÖ±ĻßM'A'µÄ½āĪöŹ½£¬“Ó¶ųĒóµĆµćP”äµÄ×ų±ź£¬“Ó¶ųĒóµĆO”¢PÖ®¼äµÄ¾ąĄė£»
£Ø2£©¹żµć![]() ×÷
×÷![]() Ę½ŠŠÓŚ
Ę½ŠŠÓŚ![]() ÖįĒŅ
ÖįĒŅ![]() £¬×÷
£¬×÷![]() µć¹ŲÓŚ
µć¹ŲÓŚ![]() ÖįµÄ¶Ō³Ęµć
ÖįµÄ¶Ō³Ęµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Ōņµć
£¬Ōņµć![]() ¼“ĪŖĖłĒó.
¼“ĪŖĖłĒó.
£Ø1£©ČēĶ¼½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£ØŅŌµć![]() ĪŖŌµć£¬
ĪŖŌµć£¬![]() ĖłŌŚÖ±ĻßĪŖ
ĖłŌŚÖ±ĻßĪŖ![]() Öį£¬“¹Ö±ÓŚ
Öį£¬“¹Ö±ÓŚ![]() µÄÖ±ĻßĪŖ
µÄÖ±ĻßĪŖ![]() Öį£©£¬ŃÓ³¤
Öį£©£¬ŃÓ³¤![]() µ½
µ½![]() Ź¹
Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬Ōņµć
£¬Ōņµć![]() ¼“ĪŖĖłĒó.
¼“ĪŖĖłĒó.

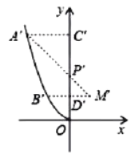
ÉčÅ×ĪļĻßµÄŗÆŹż½āĪöŹ½ĪŖ![]() £¬
£¬
ÓÉĢāŅāÖŖŠż×Ŗŗóµć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() .“ųČė½āĪöŹ½µĆ
.“ųČė½āĪöŹ½µĆ![]()
![]() Å×ĪļĻßµÄŗÆŹż½āĪöŹ½ĪŖ£ŗ
Å×ĪļĻßµÄŗÆŹż½āĪöŹ½ĪŖ£ŗ![]() £¬
£¬
µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬
![]() µć
µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬
![]()
![]() µć
µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]()
“śČė![]() £¬
£¬![]() ĒóµĆÖ±Ļß
ĒóµĆÖ±Ļß![]() µÄŗÆŹż½āĪöŹ½ĪŖ
µÄŗÆŹż½āĪöŹ½ĪŖ![]() £¬
£¬
°Ń![]() “śČė
“śČė![]() £¬µĆ
£¬µĆ![]() £¬
£¬
![]() µć
µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬
![]() ÓĆĮĻ×īŹ”Ź±£¬µć
ÓĆĮĻ×īŹ”Ź±£¬µć![]() ”¢
”¢![]() Ö®¼äµÄ¾ąĄėŹĒ
Ö®¼äµÄ¾ąĄėŹĒ![]() Ć×.
Ć×.
£Ø2£©¹żµć![]() ×÷
×÷![]() Ę½ŠŠÓŚ
Ę½ŠŠÓŚ![]() ÖįĒŅ
ÖįĒŅ![]() £¬×÷
£¬×÷![]() µć¹ŲÓŚ
µć¹ŲÓŚ![]() ÖįµÄ¶Ō³Ęµć
ÖįµÄ¶Ō³Ęµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Ōņµć
£¬Ōņµć![]() ¼“ĪŖĖłĒó.
¼“ĪŖĖłĒó.
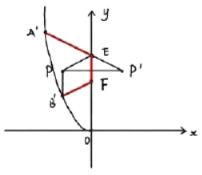
![]()
![]() µć
µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬
![]() µć×ų±źĪŖ
µć×ų±źĪŖ![]()
“śČė![]() £¬
£¬![]() £¬µÄ×ų±źĒóµĆÖ±Ļß
£¬µÄ×ų±źĒóµĆÖ±Ļß![]() µÄŗÆŹż½āĪöŹ½ĪŖ
µÄŗÆŹż½āĪöŹ½ĪŖ![]() £¬
£¬
°Ń![]() “śČė
“śČė![]() £¬µĆ
£¬µĆ![]() £¬
£¬
![]() µć
µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬
![]() ÓĆĮĻ×īŹ”Ź±£¬µć
ÓĆĮĻ×īŹ”Ź±£¬µć![]() ”¢
”¢![]() Ö®¼äµÄ¾ąĄėŹĒ
Ö®¼äµÄ¾ąĄėŹĒ![]() Ć×.
Ć×.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖÕĘĪÕ°ĖÄź¼¶ŹżŃ§æ¼ŹŌ¾ķµÄĆüĢāÖŹĮæÓėÄѶČĻµŹż£¬ĆüĢā×é½ĢŹ¦ø°ĶāµŲєȔŅ»øöĖ®Ę½Ļąµ±µÄ°ĖÄź¼¶°ą¼¶½ųŠŠŌ¤²ā£¬½«æ¼ŹŌ³É¼Ø·Ö²¼Ēéæö½ųŠŠ“¦Ąķ·ÖĪö£¬ÖĘ³ÉʵŹż·Ö²¼±ķČēĻĀ(³É¼ØµĆ·Ö¾łĪŖÕūŹż)£ŗ
×鱚 | ³É¼Ø·Ö×é | ʵŹżĘµĀŹ | ʵŹż |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
ŗĻ¼Ę | 40 | 1.00 |
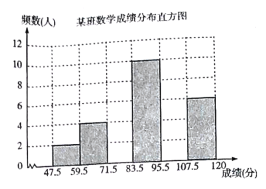
øł¾Ż±ķÖŠĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĘµŹż·Ö²¼±ķÖŠµÄ![]() £¬
£¬![]() £¬
£¬![]() £»
£»
£Ø2£©ŅŃÖŖČ«Ēų°ĖÄź¼¶¹²ÓŠ200øö°ą(Ę½¾łĆæ°ą40ČĖ)£¬ÓĆÕā·ŻŹŌ¾ķ¼ģ²ā£¬108·Ö¼°ŅŌÉĻĪŖÓÅŠć£¬Ō¤¼ĘÓÅŠćµÄČĖŹżŌ¼ĪŖ £¬72·Ö¼°ŅŌÉĻĪŖ¼°øń£¬Ō¤¼Ę¼°øńµÄČĖŹżŌ¼ĪŖ £¬¼°øńµÄ°Ł·Ö±ČŌ¼ĪŖ £»
£Ø3£©²¹³äĶźÕūʵŹż·Ö²¼Ö±·½Ķ¼.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
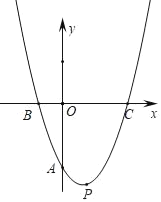
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy£½x£Øx©b£©©![]() ÓėyÖįĻą½»ÓŚAµć£¬ÓėxÖįĻą½»ÓŚB”¢CĮ½µć£¬ĒŅµćCŌŚµćBµÄÓŅ²ą£¬ÉčÅ×ĪļĻߵĶ„µćĪŖP£®
ÓėyÖįĻą½»ÓŚAµć£¬ÓėxÖįĻą½»ÓŚB”¢CĮ½µć£¬ĒŅµćCŌŚµćBµÄÓŅ²ą£¬ÉčÅ×ĪļĻߵĶ„µćĪŖP£®
£Ø1£©ČōµćBÓėµćC¹ŲÓŚÖ±Ļßx£½1¶Ō³Ę£¬ĒóbµÄÖµ£»
£Ø2£©ČōOB£½OA£¬Ēó”÷BCPµÄĆ껿£»
£Ø3£©µ±©1”Üx”Ü1Ź±£¬øĆÅ×ĪļĻßÉĻ×īøßµćÓė×īµĶµćׯ×ų±źµÄ²īĪŖh£¬Ēó³öhÓėbµÄ¹ŲĻµ£»ČōhÓŠ×ī“óÖµ»ņ×īŠ”Öµ£¬Ö±½ÓŠ“³öÕāøö×ī“óÖµ»ņ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ACĪŖŌ²OµÄÖ±¾¶£¬ĻŅADµÄŃÓ³¤ĻßÓė¹żµćCµÄĒŠĻß½»ÓŚµćB£¬EĪŖBCÖŠµć£¬AC= ![]() £¬BC=4.
£¬BC=4.
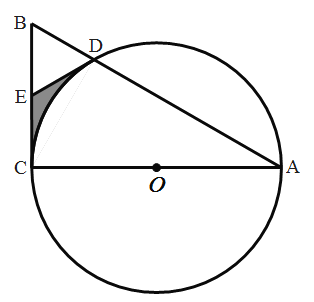
£Ø1£©ĒóÖ¤£ŗDEĪŖŌ²OµÄĒŠĻߣ»
£Ø2£©ĒóŅõÓ°²æ·ÖĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
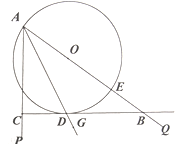
”¾ĢāÄæ”æČēĶ¼£¬AGŹĒ”ĻPAQµÄĘ½·ÖĻߣ¬µćEŌŚAQÉĻ£¬ŅŌAEĪŖÖ±¾¶µÄ”Ń0½»AGÓŚµćD£¬¹żµćD×÷APµÄ“¹Ļߣ¬“¹×ćĪŖµćC£¬½»AQÓŚµćB.
£Ø1£©ĒóÖ¤£ŗÖ±ĻßBCŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ6£¬AC=2CD£¬ĒóBDµÄ³¤
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
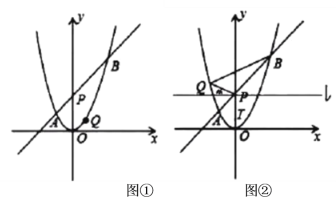
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]() µÄ¶Ō³ĘÖįĪŖÖ±Ļß
µÄ¶Ō³ĘÖįĪŖÖ±Ļß![]() £¬½«Ö±Ļß
£¬½«Ö±Ļß![]() ČĘ×ŵć
ČĘ×ŵć![]() Ė³Ź±ÕėŠż×Ŗ
Ė³Ź±ÕėŠż×Ŗ![]() µÄ¶ČŹżŗóÓėøĆÅ×ĪļĻß½»ÓŚ
µÄ¶ČŹżŗóÓėøĆÅ×ĪļĻß½»ÓŚ![]() Į½µć£Øµć
Į½µć£Øµć![]() ŌŚµć
ŌŚµć![]() µÄ×ó²ą£©£¬µć
µÄ×ó²ą£©£¬µć![]() ŹĒøĆÅ×ĪļĻßÉĻŅ»µć
ŹĒøĆÅ×ĪļĻßÉĻŅ»µć
£Ø1£©Čō![]() £¬ĒóÖ±Ļß
£¬ĒóÖ±Ļß![]() µÄŗÆŹż±ķ“ļŹ½
µÄŗÆŹż±ķ“ļŹ½
£Ø2£©Čōµć![]() ½«Ļ߶Ī·Ö³É
½«Ļ߶Ī·Ö³É![]() µÄĮ½²æ·Ö£¬Ēóµć
µÄĮ½²æ·Ö£¬Ēóµć![]() µÄ×ų±ź
µÄ×ų±ź
£Ø3£©ČēĶ¼¢Ś£¬ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬Čōµć![]() ŌŚ
ŌŚ![]() Öį×ó²ą£¬¹żµć
Öį×ó²ą£¬¹żµć![]() ×÷Ö±Ļß
×÷Ö±Ļß![]() Öį£¬µć
Öį£¬µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬ĒŅĪ»ÓŚ
ÉĻŅ»µć£¬ĒŅĪ»ÓŚ![]() Öį×ó²ą£¬µ±ŅŌ
Öį×ó²ą£¬µ±ŅŌ![]() £¬
£¬![]() £¬
£¬![]() ĪŖ¶„µćµÄČż½ĒŠĪÓė
ĪŖ¶„µćµÄČż½ĒŠĪÓė![]() ĻąĖĘŹ±£¬Ēó
ĻąĖĘŹ±£¬Ēó![]() µÄ×ų±ź
µÄ×ų±ź
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠÓŠµć
ÖŠÓŠµć![]() ŗĶijŅ»ŗÆŹżĶ¼Ļó
ŗĶijŅ»ŗÆŹżĶ¼Ļó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ÖįµÄ“¹Ļߣ¬½»Ķ¼Ļó
ÖįµÄ“¹Ļߣ¬½»Ķ¼Ļó![]() ÓŚµć
ÓŚµć![]() £¬Éčµć
£¬Éčµć![]() £¬
£¬![]() µÄׯ×ų±ź·Ö±šĪŖ
µÄׯ×ų±ź·Ö±šĪŖ![]() £¬
£¬![]() £®Čē¹ū
£®Čē¹ū![]() £¬ÄĒĆ“³Ęµć
£¬ÄĒĆ“³Ęµć![]() ĪŖĶ¼Ļó
ĪŖĶ¼Ļó![]() µÄÉĻĪ»µć£»Čē¹ū
µÄÉĻĪ»µć£»Čē¹ū![]() £¬ÄĒĆ“³Ęµć
£¬ÄĒĆ“³Ęµć![]() ĪŖĶ¼Ļó
ĪŖĶ¼Ļó![]() µÄĶ¼ÉĻµć£»Čē¹ū
µÄĶ¼ÉĻµć£»Čē¹ū![]() £¬ÄĒĆ“³Ęµć
£¬ÄĒĆ“³Ęµć![]() ĪŖĶ¼Ļó
ĪŖĶ¼Ļó![]() µÄĻĀĪ»µć£®
µÄĻĀĪ»µć£®
£Ø1£©ŅŃÖŖÅ×ĪļĻß![]() .
.
¢Ł ŌŚµćA(-1£¬0)£¬B(0£¬-2)£¬C(2£¬3)ÖŠ£¬ŹĒÅ×ĪļĻßµÄÉĻĪ»µćµÄŹĒ £»
¢Ś Čē¹ūµć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() µÄĶ¼ÉĻµć£¬ĒŅĪŖÅ×ĪļĻßµÄÉĻĪ»µć£¬Ēóµć
µÄĶ¼ÉĻµć£¬ĒŅĪŖÅ×ĪļĻßµÄÉĻĪ»µć£¬Ēóµć![]() µÄŗį×ų±ź
µÄŗį×ų±ź![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø2£©½«Ö±Ļß![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ĻĀ·½µÄ²æ·ÖŃŲÖ±Ļß
ĻĀ·½µÄ²æ·ÖŃŲÖ±Ļß![]() ·ÕŪ£¬Ö±Ļß
·ÕŪ£¬Ö±Ļß![]() µÄĘäÓą²æ·Ö±£³Ö²»±ä£¬µĆµ½Ņ»øöŠĀµÄĶ¼Ļ󣬼Ē×÷Ķ¼Ļó
µÄĘäÓą²æ·Ö±£³Ö²»±ä£¬µĆµ½Ņ»øöŠĀµÄĶ¼Ļ󣬼Ē×÷Ķ¼Ļó![]() £®”Ń
£®”Ń![]() µÄŌ²ŠÄ
µÄŌ²ŠÄ![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬°ė¾¶ĪŖ
ÖįÉĻ£¬°ė¾¶ĪŖ![]() £®Čē¹ūŌŚĶ¼Ļó
£®Čē¹ūŌŚĶ¼Ļó![]() ŗĶ”Ń
ŗĶ”Ń![]() ÉĻ·Ö±š“ęŌŚµć
ÉĻ·Ö±š“ęŌŚµć![]() ŗĶµćF£¬Ź¹µĆĻ߶ĪEFÉĻĶ¬Ź±“ęŌŚĶ¼Ļó
ŗĶµćF£¬Ź¹µĆĻ߶ĪEFÉĻĶ¬Ź±“ęŌŚĶ¼Ļó![]() µÄÉĻĪ»µć£¬Ķ¼ÉĻµćŗĶĻĀĪ»µć£¬ĒóŌ²ŠÄ
µÄÉĻĪ»µć£¬Ķ¼ÉĻµćŗĶĻĀĪ»µć£¬ĒóŌ²ŠÄ![]() µÄŗį×ų±ź
µÄŗį×ų±ź![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
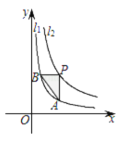
”¾ĢāÄæ”æČēĶ¼£¬ŗÆŹż![]() (x>0)ŗĶ
(x>0)ŗĶ![]() (x>0)µÄĶ¼Ļó·Ö±šŹĒ
(x>0)µÄĶ¼Ļó·Ö±šŹĒ![]() ŗĶ
ŗĶ![]() .ÉčµćPŌŚ
.ÉčµćPŌŚ![]() ÉĻ£¬PA”ĪyÖį½»
ÉĻ£¬PA”ĪyÖį½»![]() ÓŚµćA£¬PB”ĪxÖį£¬½»
ÓŚµćA£¬PB”ĪxÖį£¬½»![]() ÓŚµćB£¬”÷PABµÄĆ껿ĪŖ£Ø £©
ÓŚµćB£¬”÷PABµÄĆ껿ĪŖ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ”ĻACD£½90”ć£¬AC£½DC£¬MNŹĒ¹żµćAµÄÖ±Ļߣ¬DB”ĶMNÓŚµćB£®

£Ø1£©ČēĶ¼£¬ĒóÖ¤£ŗBD+AB£½![]() BC£»
BC£»
£Ø2£©Ö±ĻßMNČʵćAŠż×Ŗ£¬ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”ĻBCD£½30”ć£¬BD£½![]() Ź±£¬ĒóBCµÄÖµ£®
Ź±£¬ĒóBCµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com