练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知点E（2，1）在二次函数y=x2-8x+m（m为常数）的图象上，则点E关于图象对称轴的对称点坐标是（　　）
    A．（4，1）B．（5，1）C．（6，1）D．（7，1）

    分析 求得对称轴，即可求得对称点．

    解答 解：由二次函数y=x2-8x+m可知对称轴为x=-$\frac{b}{2a}$=-$\frac{-8}{2×1}$=4，
    ∵点E（2，1）与点（6，1）关于图象对称轴对称，
    ∴点E关于图象对称轴的对称点坐标是（6，1），
    故选C．

    点评 本题考查了二次函数图象上点的坐标特征，二次函数的性质，求得对称轴是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．一个三角形的两边长为3和6，若第三边取奇数，则此三角形的周长为14或16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，已知正方形ABCD的边长是4cm，点E是CD的中点，连结AE，点M是AE的中点，过点M任意作直线分别与边AD、BC相交于点P、Q．若PQ=AE，则AP=$\frac{5}{2}$或$\frac{3}{2}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，在矩形ABCD中，AB=5，BC=6，点E是AD上一点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰落在∠ADC的平分线上时，DA1=2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在Rt△AOB中，OA=3，sinB=$\frac{3}{5}$，P、M、分别是BA、BO边上的两个动点．点M从点B出发，沿BO以1单位/秒的速度向点O运动；点P从点B出发，沿BA以a单位/秒的速度向点A运动；P、M两点同时出发，任意一点先到达终点时，两点停止运动．设运动的时间为t．
    （1）线段AP的长度为5-at（用含a、t的代数式表示）；
    （2）如图①，连结PO、PM，若a=1，△PMO的面积为S，试求S的最大值；
    （3）如图②，连结PM、AM，试探究：在点P、M运动的过程中，是否存在某个时刻，使得△PMB为直角三角形且△PMA是等腰三角形？若存在，求出此时a和t的取值，若不存在，请说明理由．

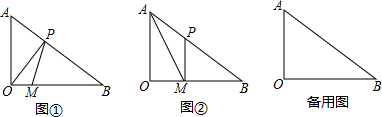
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．
    （1）如图，△OAB是抛物线y=-x2+bx（b＞0）的“抛物线三角形”，当OA=OB时，求b的值；
    （2）若抛物线y=a（x-2）2+b（a＞0，b＜0）的“抛物线三角形”是直角三角形，求a，b满足的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，在矩形纸片ABCD中，BC=40cm，AB=16cm，M点为BC边上的中点，点G沿B→A→D运动（不含端点），将矩形纸片沿直线MG翻折，使得点B落在AD边上，则折痕长度为10$\sqrt{5}$cm或8$\sqrt{5}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．一铁路路基横断面为等腰梯形ABCD，斜坡BC的坡度为i=2：3，路基高AE为3米，底CD宽12米，求路基顶AB的宽．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，△ABC是等边三角形，AB=2，D是边BC的中点，点P从点A出发，沿AB-BD以每秒1个单位长度的速度向终点D运动．同时点Q从点C出发，沿CA-AC以每秒1个单位长度的速度运动．当点P停止运动时，点Q也随之停止运动，设点P的运动时间为t（秒），△PQD的面积为S．
    （1）求线段PB的长（用含t的代数式）．
    （2）当△PQD是等边三角形时，求t的值．
    （3）当S＞0时，求S与t的函数关系式．
    （4）若点D关于直线PQ的对称点为点D′，且S＞0，直接写出点D′落在△ABC的边上时t的值．

    查看答案和解析>>

    同步练习册答案