
【题目】问题提出:
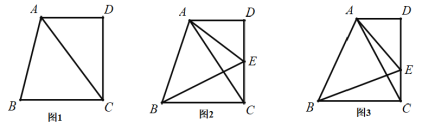
(1)如图1,在四边形![]() 中,已知:
中,已知:![]() ,
,![]() ,
,![]() ,
,![]() 的面积为8,求
的面积为8,求![]() 边上的高.
边上的高.
问题探究
(2)如图2在(1)的条件下,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的面积
的面积
问题解决
(3)如图3,在(1)的条件下,点![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 的面积是否存在最小值;若存在,求出最小值;若不存在;请说明理由.
的面积是否存在最小值;若存在,求出最小值;若不存在;请说明理由.
【答案】(1)4;(2)![]() ;(3)存在,最小值为
;(3)存在,最小值为![]()
【解析】
(1)作BC边上的高AM,利用三角形面积公式即可求解;
(2)延长DA,过B点作BF⊥DA于点F,作BH⊥AE于点H,易得四边形BCDF为矩形,在(1)的条件下BC=CD=4,则BCDF为正方形,由![]() ,结合∠FAB=∠CBA可得∠FAB=∠EAB,从而推出BF=BH=4,易证Rt△BCE≌Rt△BHE,所以EH=CE=2,设AD=a,则AF=AH=4-a,在Rt△ADE中利用勾股定理建立方程可求出a,最后根据S△ABE=
,结合∠FAB=∠CBA可得∠FAB=∠EAB,从而推出BF=BH=4,易证Rt△BCE≌Rt△BHE,所以EH=CE=2,设AD=a,则AF=AH=4-a,在Rt△ADE中利用勾股定理建立方程可求出a,最后根据S△ABE=![]() 即可求解;
即可求解;
(3)辅助线同(2),设AD=a,CE=m,则DE=4-m,同(2)可得出m与a的关系式,设△ABE的面积为y,由y=![]() 得到m与y的关系式,再求y的最小值即可.
得到m与y的关系式,再求y的最小值即可.
(1)如图所示,作BC边上的高AM,
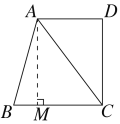
∵S△ABC=![]()
∴![]()
即BC边上的高为4;
(2)如图所示,延长DA,过B点作BF⊥DA于点F,作BH⊥AE于点H,
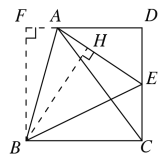
∵![]() ,
,![]()
∴∠BCD=∠D=90°=∠F
∴四边形BCDF为矩形,
又∵BC=CD=4
∴四边形BCDF为正方形,
∴DF=BF=BC=4,
又∵AD∥BC
∴∠FAB=∠CBA
又∵∠EAB=∠CBA
∴∠FAB=∠EAB
∵BF⊥AF,BH⊥AE
∴BH=BF=4,
在Rt△BCE和Rt△BHE中,
∵BE=BE,BH=BC=4
∴Rt△BCE≌Rt△BHE(HL)
∴EH=CE=2
同理可证Rt△BAF≌Rt△BAH(HL)
∴AF=AH
设AD=a,则AF=AH=4-a
在Rt△ADE中,AD=a,DE=2,AE=AH+EH=4-a+2=6-a
由勾股定理得AD2+DE2=AE2,即![]()
解得![]()
∴AE=6-a=![]()
S△ABE=![]()
(3)存在,
如图所示,延长DA,过B点作BF⊥DA于点F,作BH⊥AE于点H,

同(2)可得CE=EH,AF=AH,
设AD=a,CE=EH=m,则DE=4-m,AF=AH=4-a
在Rt△ADE中,AD2+DE2=AE2,即![]()
整理得![]()
∴AE=AH+HE=![]()
设△ABE的面积为y,
则y=![]()
∴![]()
整理得:![]()
∵方程必有实数根
∴![]()
整理得![]()
∴![]() (注:利用求根公式进行因式分解)
(注:利用求根公式进行因式分解)
又∵面积y≥0
∴![]()
即△ABE的面积最小值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知点![]() 和点
和点![]() 在抛物线
在抛物线![]() 上.
上.
(Ⅰ)求该抛物线的解析式和顶点坐标,并求出![]() 的值;
的值;
(Ⅱ)求点![]() 关于
关于![]() 轴对称点
轴对称点![]() 的坐标,并在
的坐标,并在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最短,求此时点
最短,求此时点![]() 的坐标;
的坐标;
(Ⅲ)平移抛物线![]() ,记平移后点
,记平移后点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为
的对应点为![]() ,点
,点![]() 是
是![]() 轴上的定点.
轴上的定点.
①当抛物线向左平移到某个位置时,![]() 最短,求此时抛物线的解析式;
最短,求此时抛物线的解析式;
②![]() 是
是![]() 轴上的定点,当抛物线向左平移到某个位置时,四边形
轴上的定点,当抛物线向左平移到某个位置时,四边形![]() 的周长最短,求此时抛物线的解析式(直接写出结果即可)
的周长最短,求此时抛物线的解析式(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=![]() S△ABC,上述结论中始终正确有 ( )
S△ABC,上述结论中始终正确有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
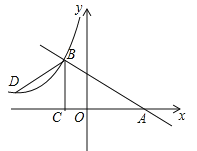
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
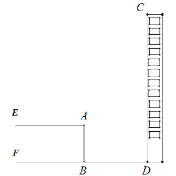
【题目】为了测量学校附近新盖大楼的高度,数学实践活动小组,借助大楼旁边高30米的空中操场进行测量.其中![]() 米,
米,![]() 地面
地面![]() ,小华站在操场的
,小华站在操场的![]() 处观测大楼顶点
处观测大楼顶点![]() 的仰角为
的仰角为![]() 、大楼底端
、大楼底端![]() 的俯角为
的俯角为![]() ,请根据题中的信息求出大楼
,请根据题中的信息求出大楼![]() 的高度.
的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市拟于中秋节前![]() 天里销售某品牌月饼,其进价为
天里销售某品牌月饼,其进价为![]() 元/
元/![]() .设第
.设第![]() 天的销售价格为
天的销售价格为![]() (元/
(元/![]() ),销售量为
),销售量为![]() .该超市根据以往的销售经验得出以下的销售规律:①当
.该超市根据以往的销售经验得出以下的销售规律:①当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 与
与![]() 满足一次函数关系,且当
满足一次函数关系,且当![]() 时,
时,![]() ;
;![]() 时,
时,![]() .②
.②![]() 与
与![]() 的关系为
的关系为![]() .
.
(1)当![]() 时,
时,![]() 与
与![]() 的关系式为 ;
的关系式为 ;
(2)![]() 为多少时,当天的销售利润
为多少时,当天的销售利润![]() (元)最大?最大利润为多少?
(元)最大?最大利润为多少?
(3)若超市希望第![]() 天到第
天到第![]() 天的日销售利润
天的日销售利润![]() (元)随
(元)随![]() 的增大而增大,则需要在当天销售价格的基础上涨
的增大而增大,则需要在当天销售价格的基础上涨![]() 元/
元/![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台州人民翘首以盼的乐清湾大桥于2018年9月28日正式通车,经统计分析,大桥上的车流速度![]() (千米/小时)是车流密度
(千米/小时)是车流密度![]() (辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当
(辆/千米)的函数,当桥上的车流密度达到220辆/千米的时候就造成交通堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米,车流速度为80千米/小时,研究证明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)求大桥上车流密度为50/辆千米时的车流速度;
(2)在某一交通高峰时段,为使大桥上的车流速度大于60千米/小时且小于80千米/小时,应把大桥上的车流密度控制在什么范围内?
(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量![]() 车流速度
车流速度![]() 车流密度,求大桥上车流量
车流密度,求大桥上车流量![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.
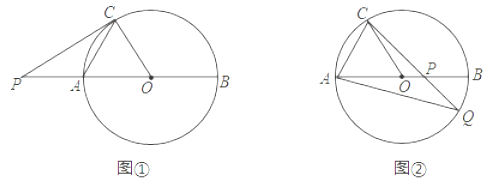
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com