
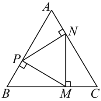
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB,MN⊥BC,PN⊥AC.
(1)求证:△PMN是等边三角形;
(2)若AB=9 cm,求CM的长度.
【答案】(1)见解析;(2)CM=3cm
【解析】
(1)根据等边三角形的性质得出∠A=∠B=∠C,进而得出∠MPB=∠NMC=∠PNA=90°,再根据平角的意义即可得出∠NPM=∠PMN=∠MNP,即可证得△PMN是等边三角形;
(2)易证得△PBM≌△MCN≌△NAP,得出PA=BM=CN,PB=MC=AN,从而求得BM+PB=AB=9cm,根据直角三角形30°角所对的直角边等于斜边的一半得出2PB=BM,即可求得PB的长,进而得出CM的长.
解:(1)∵△ABC是正三角形,
∴∠A=∠B=∠C,
∵MP⊥AB,MN⊥BC,PN⊥AC,
∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,
∴∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形;
(2)根据题意△PBM≌△MCN≌△NAP,
∴PA=BM=CN,PB=MC=AN,
∴BM+PB=AB=9cm,
∵△ABC是正三角形,
∴∠A=∠B=∠C=60°,
∴2PB=BM,
∴2PB+PB=9cm,
∴PB=3cm,
∴CM=3cm.


科目:初中数学 来源: 题型:
【题目】为响应区“美丽广西 清洁乡村”的号召,某校开展“美丽广西 清洁校园”的活动,该校经过精心设计,计算出需要绿化的面积为498m2 , 绿化150m2后,为了更快的完成该项绿化工作,将每天的工作量提高为原来的1.2倍.结果一共用20天完成了该项绿化工作.该项绿化工作原计划每天完成多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其中部分图象如图所示,下列结论错误的是( )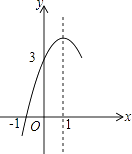
A.4ac<b2
B.方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
C.当y>0时,x的取值范围是﹣1≤x<3
D.当x<0时,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
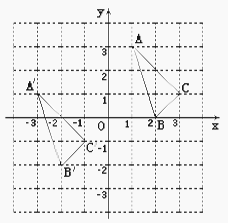
(1)分别写出下列各点的坐标:
![]() ________,
________, ![]() ________,
________, ![]() ________;
________;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:________;
经过怎样的平移得到:________;
(3)若点 ![]() (
( ![]() ,
,![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后![]() 内的对应点
内的对应点 ![]() 的坐标为________;
的坐标为________;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定:出租车起步价允许行驶的最远路程为3km,超过3km的部分每千米另收费,甲说:“我乘这种出租车走了9km,付了14元.”乙说:“我乘这种出租车走了13千米,付了20元”.请你算出这种出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
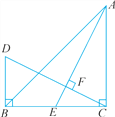
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(2,﹣2),B(6,﹣2),动点P从点O出发,沿着x轴正方向以每秒2个单位的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<4).△OPQ与四边形OABC重叠部分的面积为S.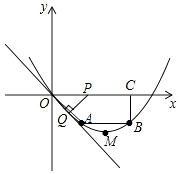
(1)求经过O、A、B三点的抛物线的解析式;
(2)若将△OPQ沿着直线PQ翻折得到△O′PQ,则当t=时,点O′恰好在抛物线上.
(3)在(2)的条件下,记△O′PQ与四边形OABC重叠的面积为S,求S与t的函数关系式,并注明自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 ![]() 的值等于 .
的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com