
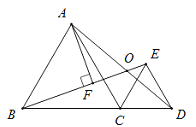
【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】C
【解析】
根据等边三角形的性质易证△BCE≌△ACD,根据全等三角形的性质可得∠CBE=∠CAD,再根据三角形外角的性质求得∠BOD=120°,即可求得∠AOF=60°,在Rt△AOF中,∠AOF=60°,OF=1,即可求得AF=![]() .
.
∵△ABC和△CDE都是等边三角形,
∴BC=AC,CE=CD,∠ACB=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,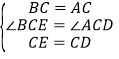 ,
,
∴△BCE≌△ACD(SAS)
∴∠CBE=∠CAD,
∵∠BOD=∠ABE+∠BAD,∠ABC=∠BAC=60°,
∴∠BOD=∠ABE+∠BAC+∠CAD=∠ABE+∠BAC+∠CBE=∠ABC+∠BAC=60°+60°=120°.
∴∠AOF=180°-∠BOD=180°-120°=60°,
在Rt△AOF中,∠AOF=60°,OF=1,
∴AF=![]() .
.
故答案为:![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生.
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数图象的顶点在原点O,经过点A(1, ![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.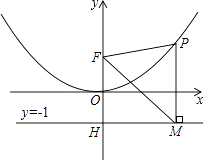
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断正误,并说明理由(1)给定一组数据,那么这组数据的众数有可能不唯一________;理由________(2)给定一组数据,那么这组数据的平均数一定是这组数据中的一个数________;
理由________(3)n个数的中位数一定是这n个数中的某一个________;理由________(4)求9个数据(x1、x2、……、x9 , 其平均数为m)的标准差S, 计算公式为:![]() ________;理由________
________;理由________
查看答案和解析>>
科目:初中数学 来源: 题型:
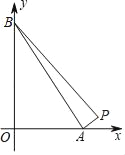
【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.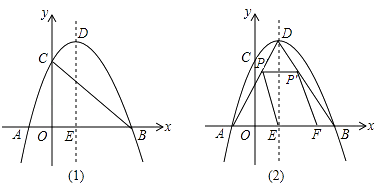
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任再次购买上述价格的钢笔和笔记本共50件作为奖品,奖励给校运动会中表现突出的同学,总费用不超过200元.请问至少要买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“美丽广西,清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元.
(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,请你写出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)如果购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵数不少于A种树苗棵数的3倍,那么有哪几种购买树苗的方案?
(3)从节约开支的角度考虑,你认为采用哪种方案更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com