
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.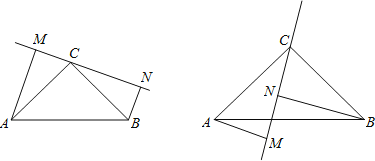
【答案】(1)见解析;(2)MN=BN-AM.理由见解析;
【解析】
(1)利用互余关系证明∠MAC=∠NCB,又∠AMC=∠CNB=90°,AC=BC,故可证△AMC≌△CNB,从而有AM=CN,MC=BN,利用线段的和差关系证明结论;
(2)类似于(1)的方法,证明△AMC≌△CNB,从而有AM=CN,MC=BN,可推出AM、BN与MN之间的数量关系.
(1)∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中
 ,
,
△AMC≌△CNB(AAS),
AM=CN,MC=NB,
∵MN=NC+CM,
∴MN=AM+BN;
(2)结论:MN=BN-AM.
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
∵∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
 ,
,
△AMC≌△CNB(AAS),
AM=CN,MC=NB,
∵MN=CM-CN,
∴MN=BN-AM.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
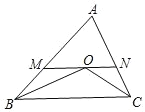
【题目】如图,在△ABC 中,∠ABC、∠ACB 的角平分线交于点 O,MN 过点 O,且MN∥BC,分别交 AB、AC 于点 M、N.若 MN=5cm,CN=2cm,则 BM=________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)
(1)若△CEF与△ABC相似,且当AC=BC=2时,求AD的长;
(2)若△CEF与△ABC相似,且当AC=3,BC=4时,求AD的长;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A. 2018 B. 2017 C. 55 D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,BD和CD为⊙O的切线,切点分别为B和C.
(1)求证:AC∥OD;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
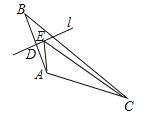
【题目】如图,在△ABC中,点D是AB边的中点,过点D作边AB的垂线l,E是l上任意一点,且AC=5,BC=8,则△AEC的周长最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如:![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() ,
,![]() 这样的分式就是真分式
这样的分式就是真分式![]() 类似的,假分式也可以化为带分式(即:整式与真分式的和的形式)
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式)
如:![]() ;
;
解决下列问题:
(1)分式![]() 是______分式(填“真分式”或“假分式”);
是______分式(填“真分式”或“假分式”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)如果x为整数,分式![]() 的值为整数,求所有符合条件的x的值.
的值为整数,求所有符合条件的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com