
【题目】已知 A(0,a),B(b,0),a、b 满足.a+b=4,a-b= 12,
(1)求 a、b 的值;
(2)在坐标轴上找一点 D,使三角形 ABD 的面积等于三角形 OAB 面积的一半, 求 D 点坐标;
(3)作∠BAO 平分线与∠ABC 平分线 BE 的反向延长线交于 P 点,求∠P 的度数.

【答案】(1)a=8,b=-4;(2)D(-2,0) 或(-8,0)或(0,4) 或(0,16);(3)45°.
【解析】
(1)根据已知列方程组即可求出a、b的值
(2)分点D在x轴上和y轴上进行解答即可
(3)根据三角形的一个外角等于与它不相邻的两个内角的和,列式求出∠ABC,再根据角平分线的定义求出∠ABE和∠BAP,然后根据三角形的一个外角等于与它不相邻的两个内角的和,列式计算即可得解.
解:(1)∵a+b=4,a-b= 12,
∴a=8,b=-4
(2)当点D在x轴上时,
∵三角形 ABD 的面积等于三角形 OAB 面积的一半,
∴D为OB的中点或BD=OB,∴D(-2,0)或(-8,0)
当点D在y轴上时,
∵三角形 ABD 的面积等于三角形 OAB 面积的一半,
∴D为OA的中点或OA=AD,∴D(0,4)或(0,16)
∴D(-2,0) 或(-8,0)或(0,4) 或(0,16)
(3)根据三角形的外角性质,可得∠ABC=∠AOB+∠BAO,
∵BE平分∠CBA,AP平分∠BAO,
∴∠ABE=![]() ∠ABC,∠BAP=
∠ABC,∠BAP=![]() ∠BAO,
∠BAO,
∴∠P=∠ABE-∠BAP=![]() (∠AOB+∠BAO)-
(∠AOB+∠BAO)-![]() ∠BAO=
∠BAO=![]() ∠AOB,
∠AOB,
∵∠AOB=90°,
∴∠P=![]() ×90°=45°.
×90°=45°.


科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
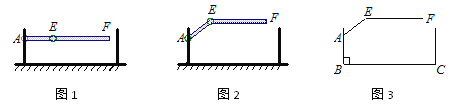
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.

(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若∠APB=150°,PA=9,PB=12,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 | A | B | C | D |
人数 | 60 | x | y | 10 |
百分比 | 30% | 50% | 15% | m |

请根据以上统计图表提供的信息,解答下列问题:
⑴本次抽查的学生有___________________名;
⑵表中x,y和m所表示的数分别为:x=________,y=______,m=_________;
⑶请补全条形统计图;
⑷根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣3|+![]() =0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
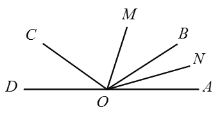
【题目】如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM和ON分别是∠AOC和∠AOB的平分线.
(1) 试说明:∠AOB=∠COD;
(2) 若∠COD=36°,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A型、B型、C型三种不同的纸板,其中A型:边长为a厘米的正方形;B型:长为a厘米,宽为1厘米的长方形;C型:边长为1厘米的正方形.
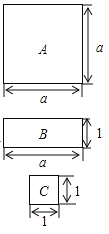
(1)A型2块,B型4块,C型4块,此时纸板的总面积为 平方厘米;
①从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形,这个大正方形的边长为 厘米;
②从这10块纸板中拿掉2块同类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形,请问拿掉的是2块哪种类型的纸板?(计算说明)
(2)A型12块,B型12块,C型4块,从这28块纸板中拿掉1块纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出三个相同形状的大正方形,则大正方形的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
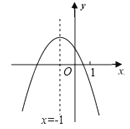
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com