
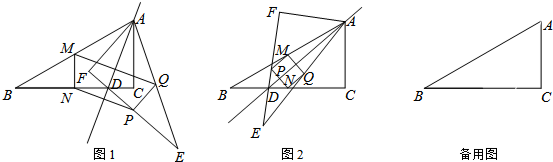
分析 (1)根据全等三角形的性质和三角形中位线定理证明即可;
(2)根据相似三角形的判定和性质得出MQ∥PN,再根据矩形的判定解答即可;
(3)直接写出图形的形状即可.
解答 解:(1)∵△ABC与△AEF关于直线AD对称,如图1,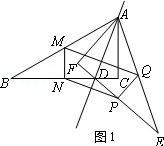
∴△ABC≌△AEF,
∴AC=AF,
∵点M、N、P、Q分别是AB、BC、EF、EA的中点,
∴MN、PQ分别是△ABC和△AEF的中位线,
∴MN=$\frac{1}{2}$AC,PQ=$\frac{1}{2}$AF,
∴MN=PQ;
(2)当BD=$\frac{1}{3}$BC时,点M、点N、点P、点Q围成的四边形是矩形.
连结BE、MN、PQ,如图2,
∵点M、点Q是AB、AE的中点.
∴MQ∥BE且MQ=$\frac{1}{2}$BE,
∵点N是BC中点,
∴BN=$\frac{1}{2}$BC,
又∵BD=$\frac{1}{3}$BC,
∴DN=BN-BD=$\frac{1}{2}$BC-$\frac{1}{3}$BC=$\frac{1}{6}$BC,
∴$\frac{DN}{BD}=\frac{1}{2}$
∵点B与点E关于直线AD对称,
∴BE⊥AD,
同理PN⊥AD,
∴BE∥PN,
∴△PDN∽△EDB,
∴$\frac{PN}{BE}=\frac{DN}{BD}=\frac{1}{2}$
∴PN∥BE,PN=$\frac{1}{2}$BE,
∴MQ∥PN且MQ=PN,
∴四边形MQNP是平行四边形,
∵MN=PQ,
∴四边形MQNP是矩形.
(3)当BD=3时,围成等腰三角形;
当BD=6时,围成矩形.
点评 此题考查几何变换问题,关键是根据全等三角形的判定和性质,以及相似三角形的性质进行分析,同时利用矩形的判定解题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
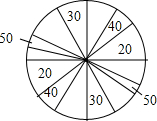 某商场搞促销活动,规定凡购物满200元就有一次摇奖机会,摇奖的转盘如图所示.转盘上写有礼券金额,其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°.计算:
某商场搞促销活动,规定凡购物满200元就有一次摇奖机会,摇奖的转盘如图所示.转盘上写有礼券金额,其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°.计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)
如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com