
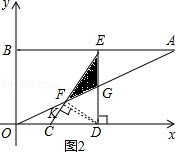
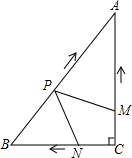
 ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.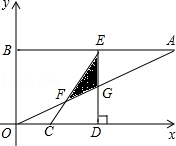
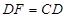 ?
?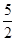 ;
;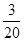 (
(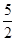 ﹣t)2,t的取值范围为:0≤t≤
﹣t)2,t的取值范围为:0≤t≤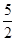 ;
;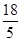 时,DF=CD;②ΔCDF的外接圆与OA相切时t=
时,DF=CD;②ΔCDF的外接圆与OA相切时t=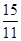 .
.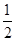 CF=
CF=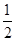 t,CK=CDcos∠DCE,由此可得出t的值;
t,CK=CDcos∠DCE,由此可得出t的值;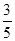 (5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OC•OD,故可得出结论.
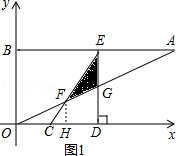
(5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OC•OD,故可得出结论. ,DE=2,
,DE=2,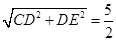 ;
;
 ,
, )=
)=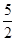 ﹣t,
﹣t,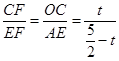 ,
, ,
,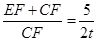 ,
,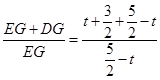 ,
,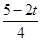 ,
,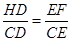 ,即HD=
,即HD= •CD=
•CD=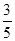 (
(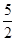 ﹣t),
﹣t),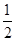 EG•HD=
EG•HD=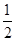 ×
×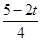 ×
×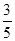 (
(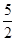 ﹣t)=
﹣t)=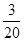 (
(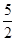 ﹣t)2,
﹣t)2,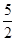 ;
;
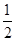 CF=
CF=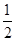 t,
t,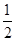 t=3×
t=3×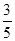 ,
,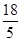 ;
;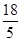 时,DF=CD;
时,DF=CD;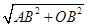 =4
=4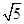 ,
,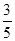 (5﹣t),
(5﹣t),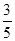 (5﹣t)=
(5﹣t)=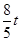 ,
,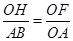 ,
,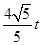 ,
,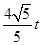 )2=t(t+3),得t=
)2=t(t+3),得t=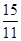 .
.

科目:初中数学 来源:不详 题型:单选题
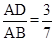 ,则EC的长是( )
,则EC的长是( )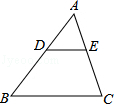
| A.4.5 | B.8 | C.10.5 | D.14 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边; |
| B.不同向量的单位向量的长度都相等,方向也都相同; |
| C.相似三角形的中线的比等于相似比; |
| D.一般来说,一条线段的黄金分割点有两个. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com