
【题目】“低碳出行,绿色出行”,自行车逐渐成为人们喜爱的交通工具,宁波某运动商城的自行车销售量自2016年起逐年增加,据统计该商城2016年销售自行车768辆,2018年销售了1200辆.
(1)若该商城近四年的自行车销售量年平均增长率相同,请你预估:该商城2019年大概能卖出多少辆自行车?
(2)考虑到自行车需求的不断增加,本月该商场准备投入3万元再购进一批两种规格的自行车,已知![]() 型车的进价为500元/辆,售价为700元/辆,
型车的进价为500元/辆,售价为700元/辆,![]() 型车的进价为1000元/辆,售价为1300元/辆.根据销售经验,
型车的进价为1000元/辆,售价为1300元/辆.根据销售经验,![]() 型车不少于
型车不少于![]() 型车的2倍,但不超过
型车的2倍,但不超过![]() 型车的3.2倍,假设所进车辆全部售完,为使得利润最大,该商场该如何进货?
型车的3.2倍,假设所进车辆全部售完,为使得利润最大,该商场该如何进货?
【答案】(1)预估该商城2019年大概能卖出1500辆自行车;(2)使利润最大,应购进![]() 型车36辆,
型车36辆,![]() 型车12辆
型车12辆
【解析】
(1)根据四年的现增长率相同和2016年销售的自行车数目,可列出方程式,解方程可得到答案;
(2) 假设进![]() 型车
型车![]() 辆,则进
辆,则进![]() 型车辆数可用含
型车辆数可用含![]() 的式子表示,根据题意得到
的式子表示,根据题意得到![]() 的取值范围,再列出利润的方程式,观察式子的特点,再
的取值范围,再列出利润的方程式,观察式子的特点,再![]() 的取值范围内找到最大值,即可得到答案.
的取值范围内找到最大值,即可得到答案.
解:(1)设该商城近四年的自行车销售量年平均增长率为![]() ,
,
则由题意可得:![]() ,
,
解得![]() ,
,![]() (舍,因为销售量逐年增加增长率不能为负数),
(舍,因为销售量逐年增加增长率不能为负数),
所以该商城近四年的自行车销售量年平均增长率为![]() .
.
2019年大概卖出![]() (辆).
(辆).
答:预估该商城2019年大概能卖出1500辆自行车.
(2)假设进![]() 型车
型车![]() 辆,则进
辆,则进![]() 型车
型车![]() 辆,根据题意得:
辆,根据题意得:
![]() ,
,
解不等式得:![]() ,利润:
,利润:
![]() .
.
因为![]() 随
随![]() 的增大而增大,又
的增大而增大,又![]() 为整数,所以
为整数,所以![]() 时,
时,![]() 最大,此时:
最大,此时:
![]() ,符合题意.
,符合题意.
答:使利润最大,应购进![]() 型车36辆,
型车36辆,![]() 型车12辆.
型车12辆.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
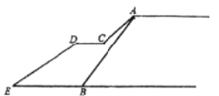
【题目】如图是重庆轻轨10号线龙头寺公园站入口扶梯建设示意图.起初工程师计划修建一段坡度为3:2的扶梯![]() ,扶梯总长为
,扶梯总长为![]() 米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建
米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建![]() 、
、![]() 两段扶梯,并减缓各扶梯的坡度,其中扶梯
两段扶梯,并减缓各扶梯的坡度,其中扶梯![]() 和平台
和平台![]() 形成的
形成的![]() 为135°,从
为135°,从![]() 点看
点看![]() 点的仰角为36.5°,
点的仰角为36.5°,![]() 段扶梯长
段扶梯长![]() 米,则
米,则![]() 段扶梯长度约为( )米(参考数据:
段扶梯长度约为( )米(参考数据:![]() ,
,![]() ,
,![]() )
)
A.43B.45C.47D.49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生参加交通安全知识网络测试活动.小华对九年(8)班全体学生的测试成绩进行了统计,并将成绩分为四个等级:优秀、良好、一般、不合格,绘制成如下的统计图(不完整),请你根据图中所给的信息解答下列问题:
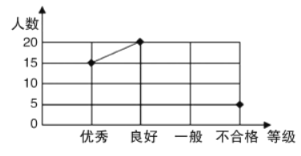
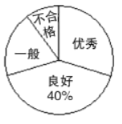
(1)九年(8)班有______名学生,并把折线统计图补充完整;
(2)已知该市共有![]() 名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;
名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;
(3)小华查了该市教育网站发现,全市参加本次测试的学生中,成绩为优秀的有![]() 人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料![]() ,乙种原料
,乙种原料![]() ,现用两种原料生产处
,现用两种原料生产处![]() 两种产品共
两种产品共![]() 件,已知生产每件
件,已知生产每件![]() 产品需甲种原料
产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获得
产品可获得![]() 元;生产每件
元;生产每件![]() 产品甲种原料
产品甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获利润
产品可获利润![]() 元,设生产
元,设生产![]() 产品
产品![]() 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产![]() 两种产品的方案有哪几种?
两种产品的方案有哪几种?
(2)设生产这![]() 件产品可获利
件产品可获利![]() 元,写出关于
元,写出关于![]() 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() ,边
,边![]() 在其所在直线上向右平移,将通过平移得到的线段记为
在其所在直线上向右平移,将通过平移得到的线段记为![]() ,连结
,连结![]() ,
,![]() ,并过点
,并过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 和
和![]() ,在平移变换过程中,设
,在平移变换过程中,设![]() 的面积为
的面积为![]() ,
,![]()
![]() ,则
,则![]() 的最大值是________.
的最大值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
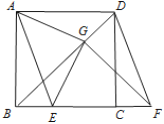
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
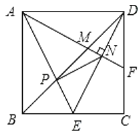
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=![]() 与直线l:y=kx+b相交于点A,B,直线l与y轴交于点P.
与直线l:y=kx+b相交于点A,B,直线l与y轴交于点P.
(1)当k=0时,求![]() 的值;
的值;
(2)点M是抛物线上的动点,过点M作MG⊥直线l于点G,当k=0时,求![]() 的值;
的值;
(3)点M是抛物线上的动点,过点M作MG∥y轴交直线l于点G,当k=2时,求证:不论b为何实数,![]() 的值为定值,并求定值;
的值为定值,并求定值;
(4)若将(2)的抛物线改为“y=ax2”,其他条件不变,则![]() 的值还为定值吗?若是,请求出定值;若不是,说明理由.
的值还为定值吗?若是,请求出定值;若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2﹣(2m+1)x+2(m≠0),请判断下列结论是否正确,并说明理由.
(1)当m<0时,函数y=mx2﹣(2m+1)x+2在x>1时,y随x的增大而减小;
(2)当m>0时,函数y=mx2﹣(2m+1)x+2图象截x轴上的线段长度小于2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 的直线与矩形
的直线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,且点
,且点![]() 不与点
不与点![]() 重合.以
重合.以![]() 为一边作菱形
为一边作菱形![]() ,点
,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,设直线
上,设直线![]() 的函数表达式为
的函数表达式为![]() .
.
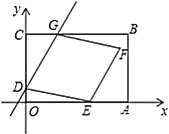
(1)当![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(2)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的长为
的长为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数表达式及自变量
的函数表达式及自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com