
【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?

【答案】此车超过每小时80千米的限制速度.
【解析】试题分析: 首先,根据在直角三角形BPO中,∠BPO=45°,可得到BO=PO=100m,再根据在直角三角形APO中,∠APO=60°,运用三角函数值,可得到AO=100![]() ,根据AB=AO-BO可求得AB的长;再结合速度的计算方法,求出车的速度,然后将车的速度与80千米/时进行比较,即可得到结论.
,根据AB=AO-BO可求得AB的长;再结合速度的计算方法,求出车的速度,然后将车的速度与80千米/时进行比较,即可得到结论.
试题解析:
解:在Rt△APO中,∠APO=60°,则∠PAO=30°.
∴AP=2OP=200 m,
AO=![]() =
=![]() =100
=100![]() (m).
(m).
在Rt△BOP中,∠BPO=45°,
则BO=OP=100 m.
∴AB=AO-BO=100![]() -100≈73(m).
-100≈73(m).
∴从A到B小车行驶的速度为73÷3≈24.3(m/s)=87.48 km/h>80 km/h.
∴此车超过每小时80千米的限制速度.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
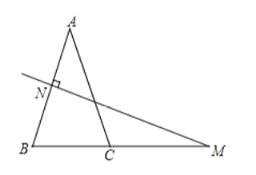
【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,则
,则![]() 为 度;
为 度;
(2)如果![]() (
(![]() ),其余条件不变,求
),其余条件不变,求![]() 的度数;
的度数;
(3)补全规律:等腰三角形一腰的垂直平分线与 相交所成的锐角等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒 ![]()
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.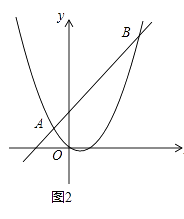
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ![]() ),B(4,0)两点.
),B(4,0)两点. 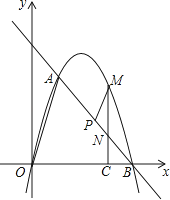
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)11![]() -1
-1![]() -1
-1![]() +4
+4![]() ;
;
(2)(-22.84)-(+38.57)+(-37.16)-(-32.57);
(3)1![]() -
-![]() +2
+2![]() +
+![]() -4
-4![]() ;
;
(4)(-36)-(-28)+(+125)+(-4)-(+53)-(-40).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com