

·ÖĪö £Ø1£©øł¾ŻÕż·½ŠĪµÄŠŌÖŹŗĶČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æɵƵ½½įĀŪ£»
£Ø2£©øł¾ŻĖıߊĪABCDŹĒĮāŠĪŗĶ”ĻABC=120”ć£¬ĶĘ³öAC”ĶBD£¬”ĻABO=60”ć£¬ĖłŅŌ”ĻFAO+”ĻAFO=90”ć£¬øł¾ŻAG”ĶBE£¬µĆµ½”ĻEAG+”ĻBEA=90”ć£¬”ĻAFO=”ĻBEA£¬ÓÖŅņĪŖ”ĻAOF=”ĻBOE=90”ć£¬ĶĘ³öČż½ĒŠĪĻąĖĘ£¬¼“æɵƵ½½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©½įĀŪ£ŗAF=BE£»
ĄķÓÉ£ŗ”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬
”ą”ĻAOB=”ĻBOC=90”ć£¬AO=BO£¬
”ßAG”ĶBE£¬”ĻAFO=”ĻBFG£¬
”ą”ĻFAO=”ĻFBG£¬
ŌŚ”÷AFOÓė”÷BFOÖŠ£¬
$\left\{\begin{array}{l}{”ĻAOF=”ĻBOE}\\{”ĻFAO=”ĻFBG}\\{AO=BO}\end{array}\right.$£¬
”ą”÷AFO”Õ”÷BFO£¬
”ąAF=BE£»
£Ø2£©½įĀŪ£ŗ$\frac{AF}{BE}$=$\sqrt{3}$£®
ĄķÓÉ£ŗ”ßĖıߊĪABCDŹĒĮāŠĪ£¬”ĻABC=120”ć£¬
”ąAC”ĶBD£¬”ĻABO=60”ć£¬
”ą”ĻFAO+”ĻAFO=90”ć£¬
”ßAG”ĶBE£¬
”ą”ĻEAG+”ĻBEA=90”ć£¬
”ą”ĻAFO=”ĻBEA£¬
Ó֔ߔĻAOF=”ĻBOE=90”ć£¬
”ą”÷AOF”×”÷BOE£¬
”ą$\frac{AF}{BE}$=$\frac{AO}{OB}$£¬
”ß”ĻABO=60”ć£¬AC”ĶBD£¬
”ą$\frac{AO}{OB}$=tan60”ć=$\sqrt{3}$£¬
”ą$\frac{AF}{BE}$=$\sqrt{3}$£®
£Ø3£©ČēĶ¼3ÖŠ£¬ŅŌABĪŖÖ±¾¶»”ŃK½»CBµÄŃÓ³¤ĻßÓŚM£®
”ßAG”ĶBE£¬
”ą”ĻAGB=90”ć£¬
”ąµćGŌŚ”ŃKÉĻ£¬
ČōµćEŌŚĻ߶ĪACÉĻŌĖ¶Æ£¬µćGµÄŌĖ¶Æ¹ģ¼£ŹĒÓÅ»”$\widehat{MOA}$£¬ÓÅ»”$\widehat{MOA}$µÄ³¤ĪŖ=$\frac{240•¦Š•1}{180}$=$\frac{4}{3}$¦Š£®
¹Ź“š°øĪŖ$\frac{4}{3}$¦Š£®
µćĘĄ ±¾Ģāæ¼²éĮĖÕż·½ŠĪµÄŠŌÖŹ£¬Č«µČČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬ĮāŠĪµÄŠŌÖŹ£¬ĻąĖĘČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬»”³¤¹«Ź½µČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įĄūÓĆĢŲŹāĪ»ÖĆ½ā¾ö½ā¾ö¹ģ¼£ĪŹĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
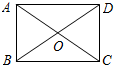 ČēĶ¼£¬¾ŲŠĪABCDµÄĮ½Ģõ¶Ō½ĒĻßĻą½»ÓŚµćO£¬”ĻAOB=60”ć£¬AB=2£¬Ōņ¾ŲŠĪµÄ±ß³¤BCµÄ³¤ŹĒ2$\sqrt{3}$£®
ČēĶ¼£¬¾ŲŠĪABCDµÄĮ½Ģõ¶Ō½ĒĻßĻą½»ÓŚµćO£¬”ĻAOB=60”ć£¬AB=2£¬Ōņ¾ŲŠĪµÄ±ß³¤BCµÄ³¤ŹĒ2$\sqrt{3}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -9 | B£® | -3 | C£® | 3 | D£® | -3»ņ3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 3øö | B£® | 4øö | C£® | 5øö | D£® | 6øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ³¤·½ŠĪABCDµÄĮ½øö¶„µć×ų±źĪŖA£Ø2£¬-1£©£¬C£Ø6£¬2£©£¬AB”ĪxÖį£¬µćMĪŖyÖįÉĻŅ»µć£¬”÷MABµÄĆ껿ĪŖ6£¬ĒŅMD£¼MA£»
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖ³¤·½ŠĪABCDµÄĮ½øö¶„µć×ų±źĪŖA£Ø2£¬-1£©£¬C£Ø6£¬2£©£¬AB”ĪxÖį£¬µćMĪŖyÖįÉĻŅ»µć£¬”÷MABµÄĆ껿ĪŖ6£¬ĒŅMD£¼MA£»²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
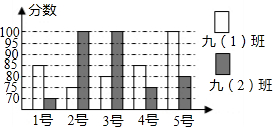 Ä³ÖŠŃ§æŖÕ¹”°³Ŗŗģøč”±øč³Ŗ±ČČü£¬¾ÅÄź¼¶£Ø1£©°ą”¢¾ÅÄź¼¶£Ø2£©°ąøł¾Ż³õČü³É¼Ø£¬ø÷Ń”³ö5ĆūŃ”ŹÖ²Ī¼Óø“Čü£¬Į½øö°ąø÷Ń”³öµÄ5ĆūŃ”ŹÖµÄø“Čü³É¼Ø£ØĀś·ÖĪŖ100·Ö£©ČēĶ¼ĖłŹ¾£ŗ
Ä³ÖŠŃ§æŖÕ¹”°³Ŗŗģøč”±øč³Ŗ±ČČü£¬¾ÅÄź¼¶£Ø1£©°ą”¢¾ÅÄź¼¶£Ø2£©°ąøł¾Ż³õČü³É¼Ø£¬ø÷Ń”³ö5ĆūŃ”ŹÖ²Ī¼Óø“Čü£¬Į½øö°ąø÷Ń”³öµÄ5ĆūŃ”ŹÖµÄø“Čü³É¼Ø£ØĀś·ÖĪŖ100·Ö£©ČēĶ¼ĖłŹ¾£ŗ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1øö | B£® | 2øö | C£® | 3øö | D£® | 4øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬”÷ABCµÄĶā½Ē”ĻACDµÄĘ½·ÖĻßÓėÄŚ½Ē”ĻABCµÄĘ½·ÖĻß½»ÓŚµćP£¬Čō”ĻBPC=41”ć£¬Ōņ”ĻCAP=50”ć£®
ČēĶ¼£¬”÷ABCµÄĶā½Ē”ĻACDµÄĘ½·ÖĻßÓėÄŚ½Ē”ĻABCµÄĘ½·ÖĻß½»ÓŚµćP£¬Čō”ĻBPC=41”ć£¬Ōņ”ĻCAP=50”ć£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com