
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为_______.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.

A. 1275 B. 2500 C. 1225 D. 1250
查看答案和解析>>
科目:初中数学 来源: 题型:
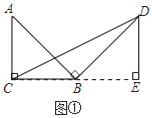
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
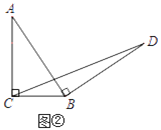
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
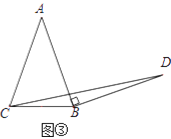
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
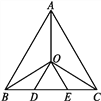
【题目】如图,在等边三角形ABC中,已知点O是三个内角平分线的交点,OD∥AB,OE∥AC,则图中等腰三角形的个数是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com