
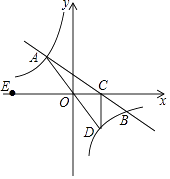
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y= ![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(12,n)
, OA=10,E为x轴负半轴上一点,且tan∠AOE= ![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)延长AO交双曲线于点D,连接CD,求△ACD的面积.
【答案】
(1)解:如图,过A作AF⊥x轴于F,
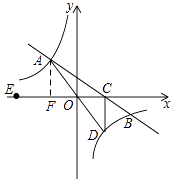
∵OA=10,tan∠AOE= ![]() ,
,
∴可设AF=4a,OF=3a,则由勾股定理可得:
(3a)2+(4a)2=102,
解得a=2,
∴AF=8,OF=6,
∴A(﹣6,8),
代入反比例函数y= ![]() ,可得m=﹣48,
,可得m=﹣48,
∴反比例函数解析式为:y=﹣ ![]() ,
,
把点B(12,n)代入y=﹣ ![]() ,可得n=﹣4,
,可得n=﹣4,
∴B(12,﹣4),
设一次函数的解析式为y=kx+b,则
![]() ,
,
解得 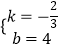 ,
,
∴一次函数的解析式为y=﹣ ![]() x+4;
x+4;
(2)解:在一次函数y=﹣ ![]() x+4中,令y=0,则x=6,即C(6,0),
x+4中,令y=0,则x=6,即C(6,0),
∵A(﹣6,8)与点D关于原点成中心对称,
∴D(6,﹣8),
∴CD⊥x轴,
∴S△ACD=S△ACO+S△CDO
= ![]() CO×AF+
CO×AF+ ![]() CO×CD
CO×CD
= ![]() ×6×8+
×6×8+ ![]() ×6×8
×6×8
=48.
【解析】(1)过A作AF⊥x轴于F,根据锐角三角函数的定义,及勾股定理得出AF=8,OF=6,进而得出A点的坐标,用待定系数法求出反比例函数的解析式,进而求出B点的坐标,再利用待定系数法求出一次函数的解析式;
(2)求出C点的坐标,根据A与点D关于原点成中心对称求出D点的坐标,然后利用S△ACD=S△ACO+S△CDO列式计算即可。


科目:初中数学 来源: 题型:
【题目】用-5、-2、1,三个数按照给出顺序构造一组无限循环数据。
(1)求第2018个数是多少?
(2)求前50个数的和是多少?
(3)试用含![]() (
(![]() 为正整数)的式子表示出数“-2所在的位置数;
为正整数)的式子表示出数“-2所在的位置数;
(4)请你算出第![]() 个,第
个,第![]() 个,第
个,第![]() 个这三个数的和?
个这三个数的和?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,且∠A=40°,那么∠ACB的外角的度数是
A. 110° B. 140° C. 110°或140° D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD的对角线相交于O,点E,F分别在边AB、BC上,且BE=BF,射线EO,FO分别交边CD、AD于G,H.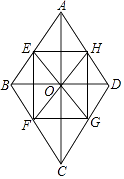
(1)求证:四边形EFGH为矩形;
(2)若OA=4,OB=3,求EG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
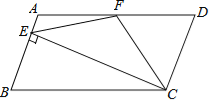
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四川汶川地震灾后重建中,某公司拟为灾区援建一所希望学校.公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的1.5倍,甲、乙两队合作完成建校工程需要72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)在施工过程中,该公司派一名技术人员在现场对施工质量进行全程监督,每天需要补助100元.若由甲工程队单独施工时平均每天的费用为0.8万元.现公司选择了乙工程队,要求其施工总费用不能超过甲工程队,则乙工程队单独施工时平均每天的费用最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简或求值
(1)若A=-2a2+ab-b3,B=a2-2ab+b3,求A -2B的值。
(2)先化简,再求值:5x2y-3xy2-7(x2y- xy![]() ),其中x=2,y=-1。
),其中x=2,y=-1。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com