
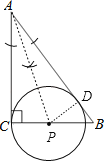
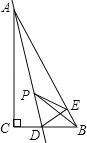
【题目】如图,△ABC中,∠C=90°.

(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)作∠BAC的平分线交BC于P点,则点P到点C的距离与点P到边AB的距离相等;
(2)作PD⊥AB于点,如图,根据角平分线性质得PD=PC,则可证明Rt△ADP≌Rt△ACP得到AD=AC=8,再利用勾股定理计算出AB=10,则BD=2,设PC=x,则PD=x,BP=6﹣x,在Rt△BDP中,利于勾股定理得(6﹣x)2=x2+22,然后解方程即可.
解:(1)如图,点P即为所求;
(2)作PD⊥AB于点,如图,
∵AP平分∠CAB,PD⊥AB于D,∠C=90°,
∴PD=PC.
在Rt△ADP和Rt△ACP中
![]() ,
,
∴Rt△ADP≌Rt△ACP(HL),
∴AD=AC=8,
在Rt△ABC中,AB=![]() =10,
=10,
∴BD=10﹣8=2,
设PC=x,则PD=x,BP=6﹣x,
在Rt△BDP中,∵PD2+BD2=PB2,
∴(6﹣x)2=x2+22,解得x=![]() .
.
答:CP的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
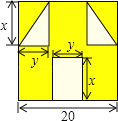
(1)用式子表示“囧”的面积S;(用含a、x、y的式子表示)
(2)当a=7,x=π,y=2时,求S(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径.
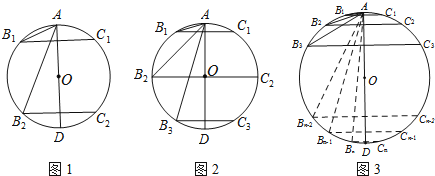
(1)如图1,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2)如图2,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,则∠B3的度数是 ;
(3)如图3,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,则∠Bn的度数是 (用含n的代数式表示∠Bn的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
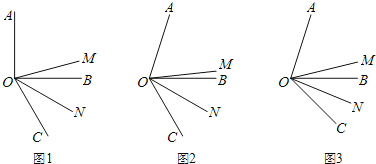
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小明上山游玩,小丽乘缆车,小明步行,两人相约在山顶的缆车终点会合.已知小明行走到缆车终点的路程是缆车到山顶的线路长的2倍,小丽在小明出发后1小时才乘上缆车,缆车的平均速度为190m/min.设小明出发x min后行走的路程为y m.图中的折线表示小明在整个行走过程中y与x的函数关系.
(1)小明行走的总路程是 m,他途中休息了 min.
(2)①当60≤x≤90时,求y与x的函数关系式;②当小丽到达缆车终点时,小明离缆车终点的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距450千米,一辆快车和一辆慢车上午7点分别从甲、乙两地以不变的速度同时出发开往乙地和甲地,快车到达乙地后休息一个小时按原速返回,快车返回甲地时已是下午5点,慢车在快车前一个小时到达甲地.试根据以上信息解答以下问题:
(1)分别求出快车、慢车的速度(单位:千米/小时);
(2)从两车出发直至慢车达到甲地的过程中,经过几小时两车相距150千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com