
【题目】如图,小蚂蚁在9×9的小方格上沿着网格线运动(每小格边长为1),一只蚂蚁在C处找到食物后,要通知A、B、D、E处的其他小蚂蚁,我们把它的行动规定:向上或向右为正,向下或向左为负。如果从C到D记为:C→D(+2,-3)(第一个数表示左、右方向,第二个数表示上、下方向),那么;

(1)C→B( ),C→E( ),D→ (-4,-3),D→ ( ,+3);
(2)若这只小蚂蚁的行走路线为C→E→D→B→A→C,请你计算小蚂蚁走过的路程.
【答案】(1)+4,-5;+7,+3;A;C,-2.(2)40.
【解析】
(1) C→B要先向右4格,再向下5格; C→E要先向右7格,再向上3格;从D开始,先向左4格,再向下3格是点A;从D开始,向上3格的线上只有点C,还需向左2格.
(2)分别求出各段路程,求和.
(1)根据向上或向右走为正,向下或向左走为负,第一个数表示左、右方向,第二个数表示上、下方向,结合图形可知C→B(+4,-5);C→E(+7,+3);(-4,-3)从D处表示向左走4个单位,向下走3个单位,观察图形可知即可到达A处;+3表示从D点向上走3个单位,观察图形,再向左走2个单位即可到达C处.
(2)根据题意,由C→E→D→B→A→C,结合图形可知:
C→E小蚂蚱走的路程为7+3=10;
E→D小蚂蚱走的路程为5+6=11;
D→B小蚂蚱走的路程为2+2=4;
B→A小蚂蚱走的路程为1+6=7;
A→C小蚂蚱走的路程为2+6=8;
所以小蚂蚱走的路程为10+11+4+7+8=40.
故答案为:(1)+4,-5;+7,+3;A;C,-2.(2)40.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①0是最小的整数;②有理数不是正数就是负数;③正整数、负整数、正分数、负分数统称为有理数;④非负数就是正数;④![]() 不仅是有理数,而且是分数;⑤
不仅是有理数,而且是分数;⑤![]() 是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
A. 7个B. 6个C. 5个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道1000米的路面下雨时经常严重积水.需改建排水系统.市政公司准备安排甲、乙两个工程队做这项工程,根据评估,有两个施工方案:
方案一:甲、乙两队合作施工,那么12天可以完成;
万案二:如果甲队先做10天,剩下的工程由乙队单独施工,还需15天才能完成.
(l)甲、乙两队单独完成此项工程各需多少天?
(2)方案一中,甲、乙两队实际各施工了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)12﹣(﹣18)+(﹣7)
(3)(+3![]() )﹣(﹣5
)﹣(﹣5![]() )+(﹣2
)+(﹣2![]() )﹣(﹣32
)﹣(﹣32![]() )
)
(4)81.26﹣293.8+8.74+111
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张丘建,我国南北朝时期(约公元5世纪)著名的数学家,著有《张丘建算经》.一次宴会上,张丘建出了一道题:“现有一只鹿向西跑,当猎人追至![]() 处时,与鹿所在的
处时,与鹿所在的![]() 处还差36步(古代:1里=300步);鹿突然向北跑,此时骑马的猎人就沿着
处还差36步(古代:1里=300步);鹿突然向北跑,此时骑马的猎人就沿着![]() 追去,追了50步至
追去,追了50步至![]() 处与鹿所在的位置
处与鹿所在的位置![]() 处还差10步(点
处还差10步(点![]() 、
、![]() 、
、![]() 在同一直线上).如果此鹿不向北转,而继续向西跑,猎人需要追多远才能追上此鹿?”,已知单位时间内鹿跑的路程和猎人骑马追赶的路程的比值是定值,请解答这个问题.
在同一直线上).如果此鹿不向北转,而继续向西跑,猎人需要追多远才能追上此鹿?”,已知单位时间内鹿跑的路程和猎人骑马追赶的路程的比值是定值,请解答这个问题.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为2的等边三角形ABC的顶点C作直线l⊥ BC,然后作△ABC关于直线l对称的△A′B′C,P为线段A′C上一动点,连接AP,PB,则AP+PB的最小值是 ( )
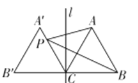
A.4B.3C.2D.2+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com