
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.

1.(1)设AE=x,四边形AMND的面积为 S,求 S关于x 的函数解析式,并指明该函数的定义域;
2.(2)当AM为何值时,四边形AMND的面积最大?最大值是多少?
3.(3)点M能是AB边上任意一点吗?请求出AM的取值范围.
1.⑴依题意,点B和E关于MN对称,则ME=MB=4-AM.
再由AM2+AE2=ME2=(4-AM)2,得AM=2- . ……………………1分
. ……………………1分
作MF⊥DN于F,则MF=AB,且∠BMF=90°.
∵MN⊥BE,∴∠ABE= 90°-∠BMN.
又∵∠FMN =∠BMF -∠BMN=90°-∠BMN,
∴∠FMN=∠ABE.
∴Rt△FMN≌Rt△ABE.
 ∴FN=AE=x,DN=DF+FN=AM+x=2-
∴FN=AE=x,DN=DF+FN=AM+x=2- +x. ………………………2分
+x. ………………………2分
∴S= (AM+DN)×AD
(AM+DN)×AD
=(2- +
+ )×4
)×4
= - +2x+8. ……………………………3分
+2x+8. ……………………………3分
其中,0≤x<4.
2.⑵∵S= - +2x+8= -
+2x+8= - (x-2)2+10,
(x-2)2+10,
∴当x=2时,S最大=10; …………………………………………5分
此时,AM=2- ×22=1.5 ………………………………………6分
×22=1.5 ………………………………………6分
答:当AM=1.5时,四边形AMND的面积最大,为10
3.⑶不能,0<AM≤2.
【解析】略


科目:初中数学 来源: 题型:
 22、如图,方格纸中每个小正方形的边长都是单位1.
22、如图,方格纸中每个小正方形的边长都是单位1.查看答案和解析>>
科目:初中数学 来源: 题型:
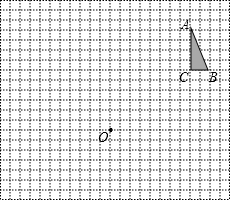 如图,方格纸中每个小正方形的边长都是单位1.
如图,方格纸中每个小正方形的边长都是单位1.查看答案和解析>>
科目:初中数学 来源: 题型:
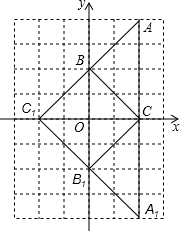 如图,方格纸中的每个小方格都是边长为1个单位的正方形.已知△ABC的顶点均在格点上,建立直角坐标系后,点A的坐标为(2,4).
如图,方格纸中的每个小方格都是边长为1个单位的正方形.已知△ABC的顶点均在格点上,建立直角坐标系后,点A的坐标为(2,4).查看答案和解析>>
科目:初中数学 来源:2015届云南省七年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点A(-1,1),现将A点先向左平移3个单位,再向下平移4个单位得到点B,然后作点B关于 轴的对称点得到C点,最后做点C关于
轴的对称点得到C点,最后做点C关于 轴的对称点得到D点。
轴的对称点得到D点。
在坐标系中作出点A、B、C、D。
顺次连接ABCDA,求四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(黑龙江牡丹江卷)数学(解析版) 题型:解答题
如图,方格纸中每个小正方形的边长都是单位1.

(1)平移已知直角三角形,使直角顶点与点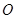 重合,画出平移后的三角形.
重合,画出平移后的三角形.
(2)将平移后的三角形绕点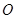 逆时针旋转
逆时针旋转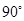 ,画出旋转后的图形.
,画出旋转后的图形.
(3)在方格纸中任作一条直线作为对称轴,画出(1)和(2)所画图形的轴对称图形,得到一个美丽的图案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com