
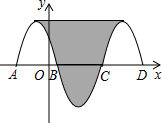
 如图,抛物线y=-x2-2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1,将Cl绕点B中心对称变换得C2,C2与x轴交于另一点C,将C2绕点C中心对称变换得C3,连接C,与C3的顶点,则图中阴影部分的面积为( )
如图,抛物线y=-x2-2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1,将Cl绕点B中心对称变换得C2,C2与x轴交于另一点C,将C2绕点C中心对称变换得C3,连接C,与C3的顶点,则图中阴影部分的面积为( )| A. | 32 | B. | 24 | C. | 36 | D. | 48 |
分析 将抛物线的一般式变形为顶点式即可得出C1的顶点坐标,由二次函数图象上点的坐标特征求出点A、B的坐标,根据中心对称的性质即可得出C2、C3的顶点坐标,再根据对称性即可得出阴影部分的面积.
解答 解:∵y=-x2-2x+3=-(x+1)2+4,
∴C1的顶点坐标为(-1,4).
当y=0时,有-x2-2x+3=0,
解得:x1=-3,x2=1,
∴点A的坐标为(-3,0),点B的坐标为(1,0).
∵将Cl绕点B中心对称变换得C2,将C2绕点C中心对称变换得C3,
∴C2的顶点坐标为(3,-4),点C的坐标为(5,0),C3的顶点坐标为(7,4),
∴S阴影=[7-(-1)]×(4-0)=8×4=32.
故选A.
点评 本题考查了抛物线与x轴的交点以及二次函数图象与几何变换,根据中心对称找出C1、C3的顶点坐标是解题的关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:选择题
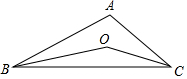 如图,△ABC中∠A=100°,BO,CO分别是∠ABC,∠ACB的角平分线且相交于O点,则∠BOC的度数为( )
如图,△ABC中∠A=100°,BO,CO分别是∠ABC,∠ACB的角平分线且相交于O点,则∠BOC的度数为( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,2cm,3cm | B. | 2cm,5cm,8cm | C. | 3cm,4cm,5cm | D. | 4cm,5cm,10cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com