
【题目】已知a、b、c在数轴上的位置如图所示,回答下列问题:
(1)化简:3|a﹣c|﹣2|﹣a﹣b|;
(2)令y=|x﹣a|+|x﹣b|+|x﹣c|,x满足什么条件时,y有最小值,求最小值
![]()
【答案】(1)a﹣2b﹣3c;(2)当x=a时y有最小值是b﹣c.
【解析】
(1)从数轴上的标示可知c<0<a<b,由此去掉绝对值符号化简即可;
(2)分区间进行去绝对值化简比较即可.
解:(1)根据数轴上的标示知,c<0<a<b,
∴a﹣c>0,﹣a﹣b<0,
∴原式=3(a﹣c)﹣2(a+b)=3a﹣3c﹣2a﹣2b
=a﹣2b﹣3c;
(2)①当x≤c时,
y=﹣x+a﹣x+b﹣x+c=﹣3x+a+b+c,
因为该函数为减函数,所以当且仅当x=c时最小,最小值为:a+b﹣2c,
②当c≤x≤a时,
y=﹣x+a﹣x+b+x﹣c=﹣x+a+b﹣c,
因为该函数为减函数,所以当且仅当x=a时最小,最小值为:b﹣c,
③当a≤x≤b时,
y=x﹣a﹣x+b+x﹣c=x﹣a+b﹣c,
因为该函数为增函数,所以当且仅当x=a时最小,最小值为:b﹣c,
④当x≥b时,
y=x﹣a+x﹣b+x﹣c=3x﹣a﹣b﹣c,
因为该函数为增函数,所以当且仅当x=b时最小,最小值为:2b﹣a﹣c,
从以上讨论中可知,当x=a时y的值是b﹣c,小于其他最小值,
所以当=a时y有最小值是b﹣c.
故答案为:(1)a﹣2b﹣3c;(2)当x=a时y有最小值是b﹣c.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
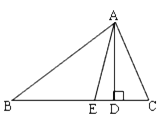
【题目】如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=40°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系 .(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
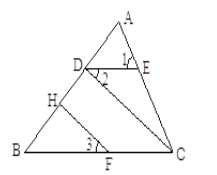
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格地面上,标有编号A,B,C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需要的时间与原计划生产450台机器所需要的时间相同.
(1)原计划平均每天生产多少台机器?
(2)若该工厂要在不超过5天的时间,生产1100台机器,则平均每天至少还要再多生产多少台机器?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 . 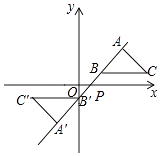
查看答案和解析>>
科目:初中数学 来源: 题型:
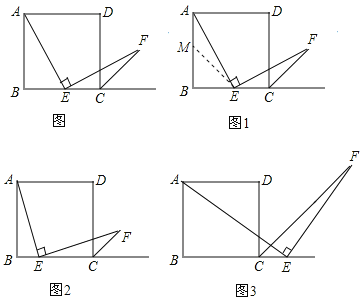
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
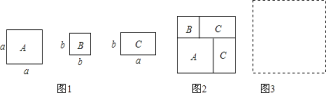
【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:______ ;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是______ ,并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com