
 如图,点O是正△ABC内一点,∠AOB=90°,∠BOC=α,将△BOC绕点C顺时针旋转60°得到△AEC,连接OE
如图,点O是正△ABC内一点,∠AOB=90°,∠BOC=α,将△BOC绕点C顺时针旋转60°得到△AEC,连接OE ?若存在请直接写出α的值,若不存在请说明理由.
?若存在请直接写出α的值,若不存在请说明理由.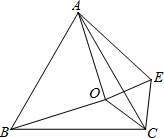 解:(1)由题意得:△BOC≌△AEC
解:(1)由题意得:△BOC≌△AEC :2时,
:2时, :2时,
:2时, =
= ,
,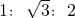 .
. :2时以及当OA:EO:AE=1:
:2时以及当OA:EO:AE=1: :2时,由勾股定理的逆定理以及锐角三角形函数关系得出α的度数即可.
:2时,由勾股定理的逆定理以及锐角三角形函数关系得出α的度数即可.

科目:初中数学 来源: 题型:
 (2012•房山区一模)已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.
(2012•房山区一模)已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
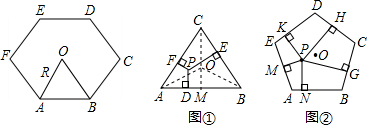 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 180° |
| n |
| 180° |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
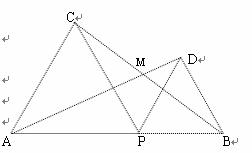
 已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.
已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,点P是线段AB上的动点,分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD,AD和BC交于点M.
(1)当△APC和△BPD面积之和最小时,直接写出AP : PB的值和∠AMC的度数;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α,当α<60°时,旋转过程中,∠AMC的度数是否发生变化?证明你的结论.
(3)在第(2)小题给出的旋转过程中,若限定60°<α<120°,∠AMC的大小是否会发生变化?若变化,请写出∠AMC的度数变化范围;若不变化,请写出∠AMC的度数.
查看答案和解析>>
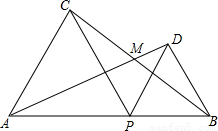
科目:初中数学 来源:2012年北京市燕山区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com