
【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
证明:∵∠BAP与∠APD互补(_________), ∴AB∥CD(____________),
∴∠BAP=∠APC(__________).
又∵∠1=∠2(__________),
∴∠BAP﹣∠1=∠APC﹣∠2(_________),即∠3=∠4,
∴AE∥PF,(___________),
∴∠E=∠F(__________).

 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
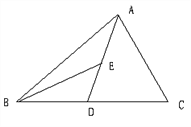
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司年前缴税20万元,今年缴税24.2万元.若该公司这两年的年均增长率相同,设这个增长率为x,则列方程( )
A.20(1+x)3=24.2
B.20(1﹣x)2=24.2
C.20+20(1+x)2=24.2
D.20(1+x)2=24.2
查看答案和解析>>
科目:初中数学 来源: 题型:
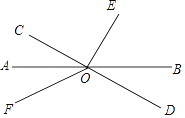
【题目】如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省乐山市第16题)在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若![]() ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数![]() 图象上点M的“可控变点”,则点M的坐标为 ;
图象上点M的“可控变点”,则点M的坐标为 ;
(2)若点P在函数![]() (
(![]() )的图象上,其“可控变点”Q的纵坐标y′的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′的取值范围是![]() ,则实数a的取值范围是 .
,则实数a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省舟山市第23题)我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”
(1)概念理解:
请你根据上述定义举一个等邻角四边形的例子;
(2)问题探究;
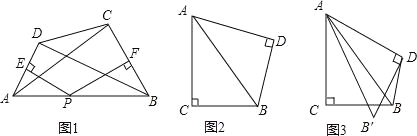
如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的中垂线恰好交于AB边上一点P,连结AC,BD,试探究AC与BD的数量关系,并说明理由;
(3)应用拓展;
如图2,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将Rt△ABD绕着点A顺时针旋转角α(0°<∠α<∠BAC)得到Rt△AB′D′(如图3),当凸四边形AD′BC为等邻角四边形时,求出它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张课桌包括1块桌面和4条桌腿,1m3木料可制作50块桌面或200条桌腿.现有5m3木料,用多少木料制作桌面,多少木料制作桌腿,才能使制作得的桌面和桌腿刚好配套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com