
(10分)如图,Rt△ABC中,<ACB=90°,AC=4,AB=5 ,点P是AC上的动点(P不与A、C重合),设PC=x,点P到AB的距离PQ为y.
(1)求y与x的函数表达式,并写出自变量x的取值范围;
(2)试讨论以P为圆心、半径长为x的圆与AB所在直线的位置关系,并指出相应的x取值范围.
解:(1)在Rt△ABC中,由勾股定理可得:BC=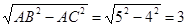 .…1分
.…1分
由题意可知:∠PQA=∠C=900,∠A=∠A,AP=AC-PC=4-x,
∴△APQ∽△ABC ∴![]() ,即:
,即: ![]() , ………………3分
, ………………3分
变形得y与x的函数表达式为:![]() ,
,
其中自变量x的取值范围为:0<x<4. ………………5分
(2)令PC=PQ,即![]() ,解得:x=
,解得:x=![]() . ………………7分
. ………………7分
∴当0<x<![]() 时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分
时,以P为圆心、半径长为x的圆与AB所在直线相离; ………………8分
当x=![]() 时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分
时, 以P为圆心、半径长为x的圆与AB所在直线相切; ………………9分
当![]() <x<4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分
<x<4时,以P为圆心、半径长为x的圆与AB所在直线相交. ………………10分
解析:略


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com