
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 根据根与系数的关系可得出ab=2,进而得出过点A的反比例函数的系数k=2,再利用反比例函数系数k的几何意义即可得出两垂线与坐标轴构成的矩形的面积的值.
解答 解:原方程可变形为x2-3x+2=0.
∵a,b是一元二次方程x(x-2)=x-2的两根,
∴ab=2.
∵点A(-a,-b)是反比例函数图象上的一个点,自点A向两坐标轴作垂线,
∴k=(-a)(-b)=ab=2,两垂线与坐标轴构成的矩形的面积S=|k|=2.
故选D.
点评 本题考查了反比例函数系数k的几何意义、反比例函数图象上点的坐标特征以及根与系数的关系,根据根与系数的关系结合反比例函数图象上点的坐标特征,找出反比例函数系数k的值是解题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.
如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
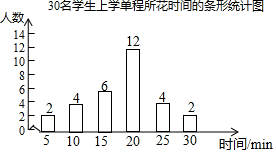 老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:
老师想知道学生每天在上学的路上要花多少时间,于是让大家将每天来学校的单程时间写在纸上.如图是全班30名学生上学单程所花时间的条形统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
一小区大门的栏杆如图所示,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )| A. | 180° | B. | 270° | C. | 300° | D. | 360° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com