
【题目】如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△Bn+1DnCn面积为Sn,则Sn等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
n+1个边长为2的等边三角形有一条边在同一直线上,则B2,B3,…Bn在一条直线上,作出直线B1B2.根据相似三角形的性质,即可求得BnDn的长,Sn与△Bn+1DnCn面积的比等于![]() ,据此即可求解.
,据此即可求解.
n+1个边长为2的等边三角形有一条边在同一直线上,则B1,B2,B3,…Bn在一条直线上,作出直线B1B2.
∴S△AB1C1=![]() ×2×
×2×![]() =
=![]() ,
,
∵∠B1C1B2=60°,
∴AB1∥B2C1,
∴△B1C1B2是等边△,且边长=2,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=![]() ,
,
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=![]() ,
,
同理:BnBn+1:ACn=1:n,
∴BnDn:DnCn=1:n,
∴Sn=![]() .
.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,活动课上,小玥想要利用所学的数学知识测量某个建筑地所在山坡AE的高度,她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1:1的斜坡按速度20米/分步行15分钟到达C处,此时,测得点A的俯角是15°.图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出建筑地所在山坡AE的高度AB.(精确到0.1米,参考数据:![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片ABCD如图折叠,B、C 两点恰好重合落在AD 边上的同一点P 处,折痕分别是MH、NG,已知∠MPN=90°,且PM=3,MN=5.则△PGN面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
(1) (思想应用)已知m, n均为正实数,且m+n=2求![]() 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
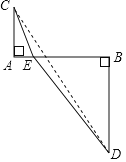
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求![]() 的最小值;
的最小值;
(2)(类比应用)根据上述的方法,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形纸片ABC中,∠ACB=90°,AC=2,BC=4,点D在边AB上,以CD为折痕将△CBD折叠得到△CPD,CP与边AB交于点E,若△DEP为直角三角形,则BD的长是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几个命题中正确的个数为 个.
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6).
②5名同学的语文成绩为90,92,92,98,103,则他们平均分为95,众数为92.
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定.
④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清楚数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.
个人年创利润/万元 | 10 | 8 | 5 | 3 |
员工人数 | 1 | 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com