
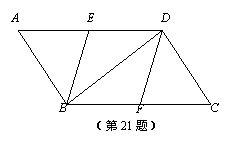
如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
若正比例函数y=2x与反比例 函数y=
函数y=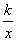 (k≠0)的图像相交,则当x<0时,交点位于( )
(k≠0)的图像相交,则当x<0时,交点位于( )
|
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:
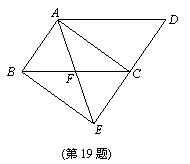
如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠ABC,连接AC、BE.求证:四边形ABEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将一条长为60 cm的卷尺铺平后折叠,使得卷尺自身的一部分重合,然后在重合部分(阴影处)沿与卷尺边 垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1︰2︰3,则折痕对应的刻度有
垂直的方向剪一刀,此时卷尺分为了三段,若这三段长度由短到长的比为1︰2︰3,则折痕对应的刻度有  ▲ 种可能.
▲ 种可能.


查看答案和解析>>
科目:初中数学 来源: 题型:
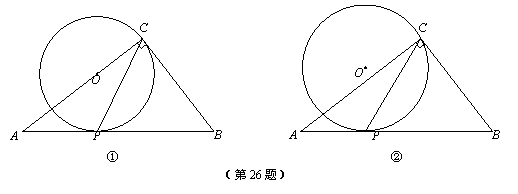
在△ABC中,∠ACB=90°,经过点C的⊙O与斜边AB相切于点P.
(1)如图①,当点O在AC上时,试说明2∠ACP=∠B;
(2)如图②,AC=8,BC=6,当点O在△ABC外部时,求CP长的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
求一元二次方程x2+3x-1=0的解,除了课本的方法外,我们也可以采用图像的方法:
在平面直角坐标系中,画出直线y=x+3和双曲线y= 的图像,则两图像交点的横坐
的图像,则两图像交点的横坐
标即该方程的解.类似地,我们可以判断方程x3-x-1=0的解的个数有( )
A.0个B. 1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.
已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,
结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货
车出发所用时间x(h)之间的函数关系图象.
(1)①请在下图中画出货车距离甲地的路程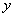 (km)与所用时间
(km)与所用时间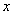 ( h)的函数关系图象;
( h)的函数关系图象;
②两车在中途相遇 次.
(2)试求货车从乙地返回甲地时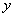 (km)与所用时间
(km)与所用时间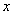 ( h)的函数关系式.
( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离
乙地多少km?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com