

| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 5 |
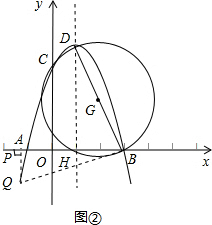 ②如图②,若∠DBQ为90°,作QP⊥x轴于P,DH⊥x轴于H
②如图②,若∠DBQ为90°,作QP⊥x轴于P,DH⊥x轴于H| DH |
| BP |
| HB |
| PQ |
| 4 |
| 3-k |
| 2 |
| k2-2k-3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
 如图③,延长DQ交y轴于M,
如图③,延长DQ交y轴于M,| DE |
| DH |
| EM |
| HB |
| 1 |
| 4 |
| EM |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |



科目:初中数学 来源:不详 题型:解答题
 只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 1,0),顶点为B.
1,0),顶点为B.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 6 |
| 5 |
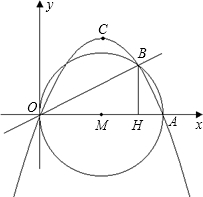 的⊙M上的两点,且tan∠AOB=
的⊙M上的两点,且tan∠AOB=| 1 |
| 2 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),⊙M与y轴的正半轴交于点C.
),⊙M与y轴的正半轴交于点C.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 24 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 项目 类别 | 年固定 成本 | 每件产品 成本 | 每件产品 销售价 | 每年最多可 生产的件数 |
| A产品 | 20 | m | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com