
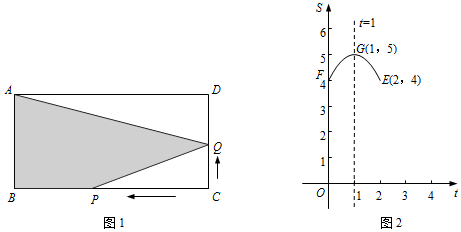
���� ��1����S��t�ĺ�����ϵʽΪ����ʽ��S=a��t-1��2+5�������E��2��4�����a=-1���ó�S��t�ĺ�����ϵʽ���ó�t��ȡֵ��Χ���ɡ�ABC������������m��ֵ��2����ͼ1��֪��S=����ABCD�����-��ADQ�����-��CPQ����������ɵó�������ϵʽ�����ɵó�����
��� �⣺��1���������ߵĶ�������Ϊ��1��5����
�����S��t�ĺ�����ϵʽΪS=a��t-1��2+5��
�����E��2��4���ã�a��2-1��2+5=4��
��ã�a=-1��
��S=-��t-1��2+5����S=-t2+2t+4��
t��ȡֵ��ΧΪ0��t��2��
�ɹ�ϵʽ�ã�F��0��4����
�൱t=0ʱ��S=4������ABC�����Ϊ4��
��$\frac{1}{2}$AB•BC=4��
��m=2��
��2����AB=6cmʱ��
��ͼ1��֪��S=����ABCD�����-��ADQ�����-��CPQ�����=4��6-$\frac{1}{2}$��4����6-t��-$\frac{1}{2}$��2t��t=-t2+2t+12����S=-��t-1��2+13��
t��ȡֵ��ΧΪ0��t��2��
��S��t�ĺ���ͼ������ɣ�1���к���ͼ������ƽ��8����λ�õ���
���� ���⿼���˶�������ĺ���ͼ���ε����ʡ���������ʽ�����Լ�����������ļ��㣻�����������ʽ�ǽ������Ĺؼ���


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
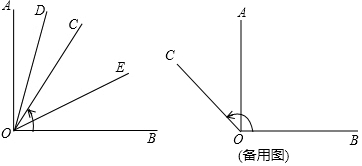
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | $\frac{1}{2}$ | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1+50%��x��80%=x-28 | B�� | ��1+50%��x��80%=x+28 | C�� | ��1+50%x����80%=x-28 | D�� | ��1-50%x����80%=x+28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͬλ����� | B�� | ���������ε����һ�������ڽ� | ||
| C�� | ����ε��ڽǺ͵���180�� | D�� | ͬ�ǻ�Ƚǵ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com